题目内容
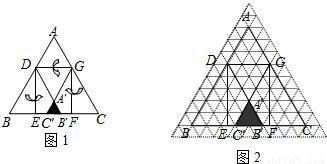
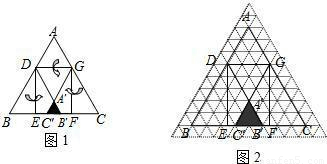
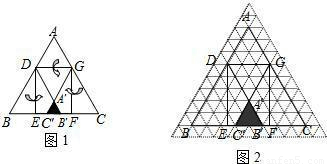
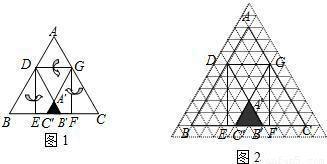
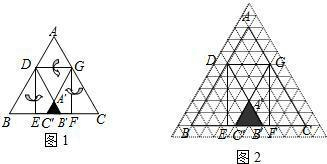
已知等边三角形纸片ABC的边长为8,D为AB边上的点,过点D作DG∥BC交AC于点G.DE⊥BC于点E,过点G作GF⊥BC于点F,把三角形纸片ABC分别沿DG,DE,GF按图1所示方式折叠,点A,B,C分别落在点A′,B′,C′处.若点A′,B′,C′在矩形DEFG内或其边上,且互不重合,此时我们称△A′B′C′(即图中阴影部分)为“重叠三角形”.(1)若把三角形纸片ABC放在等边三角形网格中(图中每个小三角形都是边长为1的等边三角形),点A,B,C,D恰好落在网格图中的格点上.如图2所示,请直接写出此时重叠三角形A′B′C′的面积;
(2)实验探究:设AD的长为m,若重叠三角形A′B′C′存在.试用含m的代数式表示重叠三角形A′B′C′的面积,并写出m的取值范围.(直接写出结果)
【答案】分析:(1)每个小三角形的面积是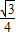 ,由图知,阴影部分有四个小三角形,故重叠三角形A'B'C'的面积为
,由图知,阴影部分有四个小三角形,故重叠三角形A'B'C'的面积为 ;
;
(2)当AD的长为m,BD为8-m,根据三角形的面积公式可得.
解答:解:(1)∵每个小三角形的面积是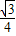
∴重叠三角形A'B'C'的面积为 ;
;
(2)重叠的等边三角形A'B'C'的边长|8-m-m|=|8-2m|,
根据S= absinC得:
absinC得:
面积是: •
•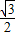 •|8-2m|2=
•|8-2m|2=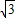 (4-m)2,
(4-m)2,
用含m的代数式表示重叠三角形A'B'C'的面积为 (4-m)2,
(4-m)2,
m的取值范围为 ≤m<4.
≤m<4.
点评:本题是一个探究性的折叠问题,考查了等边三角形的性质、图形的折叠、平行四边形的性质等,同时考核了学生对新知识的探究能力.本题题目较长,理解题意是解决本题的关键.
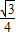 ,由图知,阴影部分有四个小三角形,故重叠三角形A'B'C'的面积为
,由图知,阴影部分有四个小三角形,故重叠三角形A'B'C'的面积为 ;
;(2)当AD的长为m,BD为8-m,根据三角形的面积公式可得.
解答:解:(1)∵每个小三角形的面积是
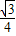
∴重叠三角形A'B'C'的面积为
 ;
;(2)重叠的等边三角形A'B'C'的边长|8-m-m|=|8-2m|,
根据S=
 absinC得:
absinC得:面积是:
 •
•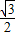 •|8-2m|2=
•|8-2m|2=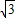 (4-m)2,
(4-m)2,用含m的代数式表示重叠三角形A'B'C'的面积为
 (4-m)2,
(4-m)2,m的取值范围为
 ≤m<4.
≤m<4.点评:本题是一个探究性的折叠问题,考查了等边三角形的性质、图形的折叠、平行四边形的性质等,同时考核了学生对新知识的探究能力.本题题目较长,理解题意是解决本题的关键.

练习册系列答案
相关题目
 三角形A′B′C′的面积,并写出m的取值范围.(直接写出结果)
三角形A′B′C′的面积,并写出m的取值范围.(直接写出结果)