题目内容
先阅读下面的材料再完成下列各题
我们知道,若二次函数y=ax2+bx+c对任意的实数x都有y≥0,则必有a>0,△=b2-4ac≤0;例如y=x2+2x+1=(x+1)2≥0,则△=b2-4ac=0,y=x2+2x+2=(x+1)2+1>0,则△=b2-4ac<0.
(1)求证:(a12+a22+…+an2)•(b12+b22+…+bn2)≥(a1•b1+a2•b2+…+an•bn)2
(2)若x+2y+3z=6,求x2+y2+z2的最小值;
(3)若2x2+y2+z2=2,求x+y+z的最大值;
(4)指出(2)中x2+y2+z2取最小值时,x,y,z的值(直接写出答案).
解:(1)构造二次函数:f(x)=(a1x+b1)2+(a2x+b2)2+…+(anx+bn)2=(a12+a22+…+an2)x2+2(a1b1+a2b2+…+anbn)x+(b12+b22+…+bn2)≥0,
∴△=4(a1b1+a2b2+…+anbn)2-4(a12+a22+…+an2)(b12+b22+…+bn2)≤0,
即:(a12+a22+…+an2)•(b12+b22+…+bn2)≥(a1•b1+a2•b2+…+an•bn)2,
当且仅当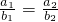 =…=
=…= 时等号成立;
时等号成立;
(2)根据(1)可得:(1+4+9)(x2+y2+z2)≥(x+2y+3z)2,
∵x+2y+3z=6,
∴14(x2+y2+z2)≥36,
∴x2+y2+z2≥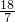 ;
;
∴若x+2y+3z=6,则x2+y2+z2的最小值为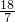 ;
;
(3)根据(1)可得:(2x2+y2+z2)( +1+1)≥(x+y+z)2,
+1+1)≥(x+y+z)2,
∵2x2+y2+z2=2,
∴(x+y+z)2≤2× =5,
=5,
∴- ≤x+y+z≤
≤x+y+z≤ ,
,
∴若2x2+y2+z2=2,则x+y+z的最大值为 ;
;
(4)∵当且仅当x= =
=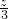 时,x2+y2+z2取最小值,
时,x2+y2+z2取最小值,
设x= =
=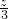 =k,
=k,
则x=k,y=2k,z=3k,
∵x+2y+3z=6,
∴k+4k+9k=6,
解得:k= ,
,
∴当x2+y2+z2取最小值时,x= ,y=
,y= ,z=
,z=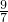 .
.
分析:(1)首先构造二次函数:f(x)=(a1x+b1)2+(a2x+b2)2+…+(anx+bn)2=(a12+a22+…+an2)x2+2(a1b1+a2b2+…+anbn)x+(b12+b22+…+bn2),由(a1x+b1)2+(a2x+b2)2+…+(anx+bn)2≥0,即可得f(x)≥0,可得△=4(a1b1+a2b2+…+anbn)2-4(a12+a22+…+an2)(b12+b22+…+bn2)≤0,整理即可证得:(a12+a22+…+an2)•(b12+b22+…+bn2)≥(a1•b1+a2•b2+…+an•bn)2;
(2)利用(1)可得:(1+4+9)(x2+y2+z2)≥(x+2y+3z)2,又由x+2y+3z=6,整理求解即可求得答案;
(3)利用(1)可得:(2x2+y2+z2)( +1+1)≥(x+y+z)2,又由2x2+y2+z2=2,整理求解即可求得答案;
+1+1)≥(x+y+z)2,又由2x2+y2+z2=2,整理求解即可求得答案;
(4)因为当且仅当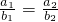 =…=
=…= 时等号成立,即可得当且仅当x=
时等号成立,即可得当且仅当x= =
=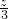 时,x2+y2+z2取最小值,又由x+2y+3z=6,即可求得答案.
时,x2+y2+z2取最小值,又由x+2y+3z=6,即可求得答案.
点评:此题考查了二次函数的综合应用.此题难度较大,解题的关键是根据题意构造二次函数f(x)=(a1x+b1)2+(a2x+b2)2+…+(anx+bn)2=(a12+a22+…+an2)x2+2(a1b1+a2b2+…+anbn)x+(b12+b22+…+bn2),然后利用判别式求解.
∴△=4(a1b1+a2b2+…+anbn)2-4(a12+a22+…+an2)(b12+b22+…+bn2)≤0,
即:(a12+a22+…+an2)•(b12+b22+…+bn2)≥(a1•b1+a2•b2+…+an•bn)2,
当且仅当
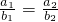 =…=
=…= 时等号成立;
时等号成立;(2)根据(1)可得:(1+4+9)(x2+y2+z2)≥(x+2y+3z)2,
∵x+2y+3z=6,
∴14(x2+y2+z2)≥36,
∴x2+y2+z2≥
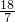 ;
;∴若x+2y+3z=6,则x2+y2+z2的最小值为
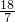 ;
;(3)根据(1)可得:(2x2+y2+z2)(
 +1+1)≥(x+y+z)2,
+1+1)≥(x+y+z)2,∵2x2+y2+z2=2,
∴(x+y+z)2≤2×
 =5,
=5,∴-
 ≤x+y+z≤
≤x+y+z≤ ,
,∴若2x2+y2+z2=2,则x+y+z的最大值为
 ;
;(4)∵当且仅当x=
 =
=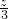 时,x2+y2+z2取最小值,
时,x2+y2+z2取最小值,设x=
 =
=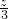 =k,
=k,则x=k,y=2k,z=3k,
∵x+2y+3z=6,
∴k+4k+9k=6,
解得:k=
 ,
,∴当x2+y2+z2取最小值时,x=
 ,y=
,y= ,z=
,z=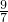 .
.分析:(1)首先构造二次函数:f(x)=(a1x+b1)2+(a2x+b2)2+…+(anx+bn)2=(a12+a22+…+an2)x2+2(a1b1+a2b2+…+anbn)x+(b12+b22+…+bn2),由(a1x+b1)2+(a2x+b2)2+…+(anx+bn)2≥0,即可得f(x)≥0,可得△=4(a1b1+a2b2+…+anbn)2-4(a12+a22+…+an2)(b12+b22+…+bn2)≤0,整理即可证得:(a12+a22+…+an2)•(b12+b22+…+bn2)≥(a1•b1+a2•b2+…+an•bn)2;
(2)利用(1)可得:(1+4+9)(x2+y2+z2)≥(x+2y+3z)2,又由x+2y+3z=6,整理求解即可求得答案;
(3)利用(1)可得:(2x2+y2+z2)(
 +1+1)≥(x+y+z)2,又由2x2+y2+z2=2,整理求解即可求得答案;
+1+1)≥(x+y+z)2,又由2x2+y2+z2=2,整理求解即可求得答案;(4)因为当且仅当
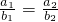 =…=
=…= 时等号成立,即可得当且仅当x=
时等号成立,即可得当且仅当x= =
=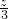 时,x2+y2+z2取最小值,又由x+2y+3z=6,即可求得答案.
时,x2+y2+z2取最小值,又由x+2y+3z=6,即可求得答案.点评:此题考查了二次函数的综合应用.此题难度较大,解题的关键是根据题意构造二次函数f(x)=(a1x+b1)2+(a2x+b2)2+…+(anx+bn)2=(a12+a22+…+an2)x2+2(a1b1+a2b2+…+anbn)x+(b12+b22+…+bn2),然后利用判别式求解.

练习册系列答案
相关题目
先阅读下面的材料,再解答后面的各题:
现代社会对保密要求越来越高,密码正在成:为人们生活的一部分.有一种密码的明文(真实文)按计算机键盘字母排列分解,其中Q、W、E、…、N、M这26个字母依次对应1,2,3…25,26这26个自然数(见下表):
给出一个变换公式:
将明文转换成密文,如:4?
+17=19,即R变为L.
11?
+8=12,即A变为S.
将密文转换成明文,如:21?3×(21-17)-2=10,即X变为P
13?3×(13-8)-1=14,即D变为F.
(1)按上述方法将明文NET译为密文;
(2)若按上述方法将明文译成的密文为DWN,请找出它的明文.
现代社会对保密要求越来越高,密码正在成:为人们生活的一部分.有一种密码的明文(真实文)按计算机键盘字母排列分解,其中Q、W、E、…、N、M这26个字母依次对应1,2,3…25,26这26个自然数(见下表):
| Q | W | E | R | T | Y | U | I | O | P | A | S | D |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| F | G | H | J | K | L | Z | X | C | V | B | N | M |
| 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 |
|
将明文转换成密文,如:4?
| 4+2 |
| 3 |
11?
| 11+1 |
| 3 |
将密文转换成明文,如:21?3×(21-17)-2=10,即X变为P
13?3×(13-8)-1=14,即D变为F.
(1)按上述方法将明文NET译为密文;
(2)若按上述方法将明文译成的密文为DWN,请找出它的明文.


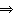
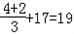 ,即R变为L.
,即R变为L.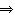
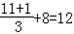 ,即A变为S.
,即A变为S.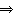 3×(21﹣17)﹣2=10,
3×(21﹣17)﹣2=10,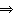 3×(13﹣8)﹣1=14,即D变为F.
3×(13﹣8)﹣1=14,即D变为F.