Question

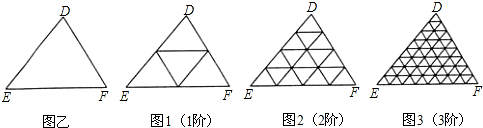
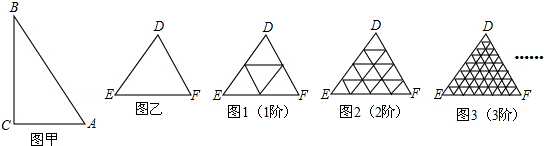
一般地，“任意三角形都是自相似图形”，只要顺次连接三角形各边中点，则可将原三角形分割为四个都与它自己相似的小三角形．我们把△DEF（图乙）第一次顺次连接各边中点所进行的分割，称为1阶分割（如图1）；把1阶分割得出的4个三角形再分别顺次连接它的各边中点所进行的分割，称为2阶分割（如图2）…，依此规则操作下去．n阶分割后得到的每一个小三角形都是全等三角形（n为正整数），设此时小三角形的面积为S_n．请写出一个反映S_n-1，S_n，S_n+1（n＞1）之间关系的等式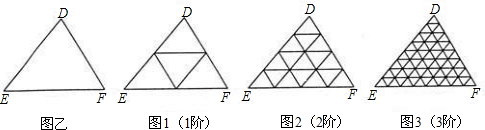

 

．

Answer 1

分析：1阶三角形有4个，把这4个三角形再分，每个分成4个，即共有4²个三角形，即2阶三角形有4²个三角形，进而可以得到n阶三角形有4ⁿ个三角形．

解答：解：设△DEF的面积是a
则S_n-1=

a

4n-1

，S_n=

a

4n

，S_n+1=

a

4n+1

根据(

a

4n

)2=

a

4n-1

•

a

4n+1

因而S_n-1，S_n，S_n+1三者之间关系式是S_n²=S_n-1•S_n+1．
∴三者之间关系式是S_n²=S_n-1•S_n+1．

点评：这是一个猜想规律的问题，解题的关键是根据规律，能判断出n阶分割后小三角形的个数．