题目内容
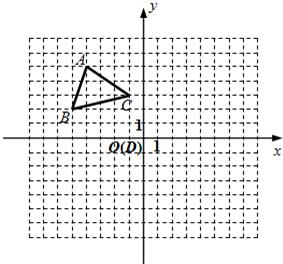26、在直角坐标系中，△ABC的三个顶点的坐标分别为A（-4，5），B（-5，2），C（-1，3）．（1）已知△A′B′C′与△ABC关于点D成中心对称．
①如图，若D点与原点（0，0）重合．请在图中画出△A′B′C′，并写出△A′B′C′三个顶点的坐标；
②若把①中的D点沿x轴向右平移1个单位，则①中的△A′BC′向右平移
2
个单位；若把①中的D点沿y轴向上平移1个单位，则①中的△A′B′C′向上平移2
个单位．（2）请用你在（1）中获得的经验直接写出A、B、C三点关于点（m，n）（m＞0，n＞0）的对称点的坐标．
分析：（1）①关于原点的中心对称，对应点横、纵坐标都互为相反数；②观察网格，可以直接得出结论；
（2）由（1）推出一般规律．
（2）由（1）推出一般规律．
解答：解：（1）①画图如下，A′（4，-5），B′（5，-2），C′（1，-3）；
②2，2；
（2）（4+2m，-5+2n），（5+2m，-2+2n），（1+2m，-3+2n）．
②2，2；
（2）（4+2m，-5+2n），（5+2m，-2+2n），（1+2m，-3+2n）．
点评：本题考查了对称中心的坐标与对称点坐标变化的关系；本题由特殊到一般，由易到难，是探讨数学问题的一般方法．
练习册系列答案
相关题目
在直角坐标系中，将坐标为（5，6），（1，2），（3，2），（3，0），（7，0），（7，2），（9，2），（5，6）的点用线段依此连接起来形成一个图案．
如图，△ABC在直角坐标系中，