题目内容
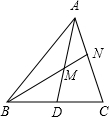 如图,D是BC的中点,M是AD的中点,BM的延长线交AC于N,则AN:NC等于
如图,D是BC的中点,M是AD的中点,BM的延长线交AC于N,则AN:NC等于
- A.1:1
- B.1:2
- C.1:3
- D.1:4
B
分析:过D作DF∥AC交BN于F,根据DF∥AC和M是AD的中点,推出DF=AN,同理得到F是BN的中点,推出DF= CN,即可求出答案.
CN,即可求出答案.
解答: 解:过D作DF∥AC交BN于F.
解:过D作DF∥AC交BN于F.
∵DF∥AC,
∴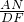 =
=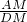 ,
,
∵M是AD的中点,
∴AM=DM,
∴DF=AN,
∵D是BC的中点,DF∥AC,
∴F是BN的中点,
∴DF= CN,
CN,
∴AN= CN,
CN,
∴AN:NC=1:2,
故选B.
点评:本题主要考查对平行线分线段成比例定理,三角形的中位线定理等知识点的理解和掌握,能通过作辅助线得到三角形的中位线是解此题的关键.
分析:过D作DF∥AC交BN于F,根据DF∥AC和M是AD的中点,推出DF=AN,同理得到F是BN的中点,推出DF=
 CN,即可求出答案.
CN,即可求出答案.解答:
 解:过D作DF∥AC交BN于F.
解:过D作DF∥AC交BN于F.∵DF∥AC,
∴
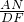 =
=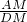 ,
,∵M是AD的中点,
∴AM=DM,
∴DF=AN,
∵D是BC的中点,DF∥AC,
∴F是BN的中点,
∴DF=
 CN,
CN,∴AN=
 CN,
CN,∴AN:NC=1:2,
故选B.
点评:本题主要考查对平行线分线段成比例定理,三角形的中位线定理等知识点的理解和掌握,能通过作辅助线得到三角形的中位线是解此题的关键.

练习册系列答案
相关题目
 16、已知:如图,E是BC的中点,∠1=∠2,∠A=∠D.
16、已知:如图,E是BC的中点,∠1=∠2,∠A=∠D.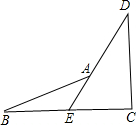 已知:如图,E是BC的中点,点A在DE上,且∠BAE=∠CDE.
已知:如图,E是BC的中点,点A在DE上,且∠BAE=∠CDE.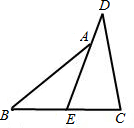 22、阅读下面的题目及分析过程,并按要求进行证明.
22、阅读下面的题目及分析过程,并按要求进行证明.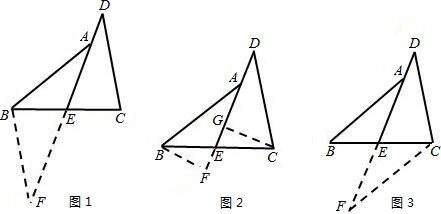
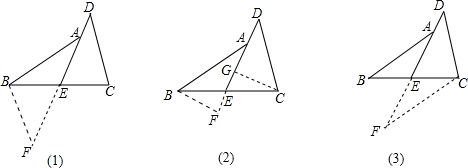
 已知:如图,E是BC的中点,∠1=∠2,AE=DE.AB和DC相等吗?请说明理由.
已知:如图,E是BC的中点,∠1=∠2,AE=DE.AB和DC相等吗?请说明理由.