题目内容
CD是⊙O的直径，AB是一条弦（AB不是直径），已知CD⊥AB，垂足为F，CD=13，AB=12，则CF的长为
- A.4或9
- B.6
- C.3或12
- D.5或9
A
分析：连接OA，求出AF、OA的值，在△AFO中根据勾股定理求出OF，求出CF和DF即可．
解答：
连接OA，
∵CD是直径，CD⊥AB，
∴AF=BF=
AB=6，OA=CD=6.5，
在Rt△OAF中，由勾股定理得：OF=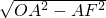
=2.5，
∴CF=OC-OF=6.5-2.5=4，
当C在D点时，CF=6.5+2.5=9，
∴CF=4或9，
故选A．
点评：本题考查了垂径定理和勾股定理的应用，关键是求出OF长，注意有两种情况啊，题目比较典型，难度适中．
分析：连接OA，求出AF、OA的值，在△AFO中根据勾股定理求出OF，求出CF和DF即可．
解答：
连接OA，
∵CD是直径，CD⊥AB，
∴AF=BF=
AB=6，OA=CD=6.5，在Rt△OAF中，由勾股定理得：OF=
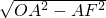=2.5，∴CF=OC-OF=6.5-2.5=4，
当C在D点时，CF=6.5+2.5=9，
∴CF=4或9，
故选A．
点评：本题考查了垂径定理和勾股定理的应用，关键是求出OF长，注意有两种情况啊，题目比较典型，难度适中．
练习册系列答案
相关题目
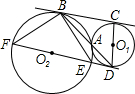，过D点作CB的平行线交⊙O2于E、F，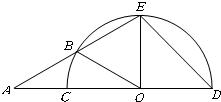
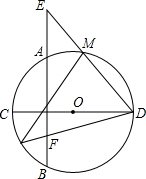如图，AB是⊙O的弦，CD是⊙O的直径，AB⊥CD，过点D作直线交BA的延长线于E，交⊙O于点M，点N为
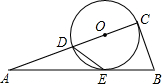（2013•河东区一模）如图，已知CD是⊙O的直径，AC⊥BC，垂足为C，点E为圆上一点，直线BE、CD相交于点A，且∠A+2∠AED=90°．
已知：如图，AB，CD是⊙O的直径，∠C=∠B，