Question

如图．一个有弹性的小球从点A下落到地面，弹起到点B后，再次落到地面又弹起到点C，已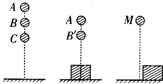知弹起的高度是前一次落下高度的80%．
（1）若点C的高度为80cm，求点A的高度？
（2）在点A的高度与（1）中相同的状态下，小球又从点A下落，落到高出地面20cm的平台上，弹起到点B'再下落（弹性不变）．求此时点B'离地面的高度？
（3）若小球从点M下落到地面，弹起到点N后，又落下至高出地面20cm的平台上，再次弹起到点P．为了使点P离地面的高度不低于80cm，则点M离地面的高度至少为多高？

Answer 1

解：（1）设点A的高度为h，则有h×80%×80%=80，
解得：h=125cm．
（2）设点B'离地面的高度为h，则A点平台的高度=（125-20）cm，点B'离地面的高度为：（125-20）×80%+20，
故（125-20）×80%+20=h，
解得：h=104cm．
（3）设点M离地面的高度至少h，则有（h×80%-20）×80%+20≥80，
解得：h≥118.75cm，
即点M离地面的高度至少118.75cm．
分析：（1）根据弹起的高度是前一次落下高度的80%，点C的高度为80cm，即可求出点A的高度；
（2）设点B'离地面的高度为h，则有（125-20）×80%+20=h，继而求出点B'离地面的高度；
（3）设点M离地面的高度至少h，则有（h×80%-20）×80%+20≥80，继而求出答案．
点评：本题考查了一元一次不等式的实际应用，及一元一次方程的应用，难度不大，关键是读懂题意列出方程和不等关系．