题目内容
如图所示，两建筑物的水平距离为s米，从A点测得D点的俯角为α，测得C点的俯角为β，则较低的建筑物的高为（ ）
A．s•tanβ米
B．s•tan（α-β）米
C．s（tanβ-tanα）米
D．
米
【答案】分析：过A点作AE∥BC，与CD延长线相交于E点．CD=CE-DE，在直角三角形中用s分别表示CE、DF得解．
解答：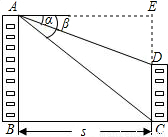
解：作AE∥BC，与CD延长线相交于E点．
由于两建筑物的水平距离为s米，从A点测得D点的俯角为α，测得C点的俯角为β，
在Rt△ACE中，CE=tanβ•s；
在Rt△ADE中，DE=tanα•s，
则CD=s（tanβ-tanα）．
故选C．
点评：本题考查俯仰角的定义，要求学生能借助俯仰角构造直角三角形并解直角三角形．
解答：
解：作AE∥BC，与CD延长线相交于E点．由于两建筑物的水平距离为s米，从A点测得D点的俯角为α，测得C点的俯角为β，
在Rt△ACE中，CE=tanβ•s；
在Rt△ADE中，DE=tanα•s，
则CD=s（tanβ-tanα）．
故选C．
点评：本题考查俯仰角的定义，要求学生能借助俯仰角构造直角三角形并解直角三角形．
练习册系列答案
相关题目
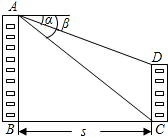如图所示，两建筑物的水平距离为s米，从A点测得D点的俯角为α，测得C点的俯角为β，则较低的建筑物的高为（ ）| A、s•tanβ米 | ||
| B、s•tan（α-β）米 | ||
| C、s（tanβ-tanα）米 | ||
D、
|
如图所示，两建筑物的水平距离为s米，从A点测得D点的俯角为α，测得C点的俯角为β，则较低的建筑物的高为
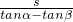米