Question

【题目】如图，∠ABM＝90°，⊙O分别切AB、BM于点D、E．AC切⊙O于点F，交BM于点C（C与B不重合）．

（1）用直尺和圆规作出AC（保留作图痕迹，不写作法）；

（2）若⊙O半径为1，AD＝4，求AC的长．

Answer 1

【答案】（1）见解析 （2）

【解析】

（1）根据题意利用尺规作图作出AC即可；
（2）先证明矩形ODBE是正方形，再利用正方形的性质和勾股定理即可解答.

（1）如图，AC即为所求；

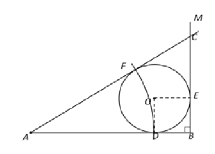
（2）解：连OD、OE．

∵ ⊙O分别切AB、BM于点D、E，

∴ OD⊥AB，OE⊥BC．

∴ ∠ODB＝90°，∠OEB＝90°．

又 ∠ABM＝90°，

∴ 四边形ODBE是矩形．

∵ OD＝OE，

∴ 矩形ODBE是正方形．

∴ BD＝BE＝OD＝1

∵ ⊙O分别切AB、AC于点D、F，

∴ AF＝AD＝4．

同理 CF＝CE

∵ Rt△ABC中，∠B＝90°，

∴ AC2＝AB2＋BC2．

即 (CE＋4)2＝(CE＋1)2＋52．

解得 CE＝．

∴ AC＝AF＋CF＝