题目内容
 如图,广安市防洪指挥部发现渠江边一处长400米,高8米,背水坡的坡角为45°的防洪大堤(横截面为梯形ABCD)急需加固.经调查论证,防洪指挥部专家组制定的加固方案是:背水坡面用土石进行加固,并使上底加宽2米,加固后,背水坡EF的坡比i=1:2.
如图,广安市防洪指挥部发现渠江边一处长400米,高8米,背水坡的坡角为45°的防洪大堤(横截面为梯形ABCD)急需加固.经调查论证,防洪指挥部专家组制定的加固方案是:背水坡面用土石进行加固,并使上底加宽2米,加固后,背水坡EF的坡比i=1:2.
(1)求加固后坝底增加的宽度AF的长;
(2)求完成这项工程需要土石多少立方米?
解:(1)分别过点E、D作EG⊥AB、DH⊥AB交AB于G、H,

∵四边形ABCD是梯形,且AB∥CD,
∴DH平行且等于EG,
故四边形EGHD是矩形,
∴ED=GH,
在Rt△ADH中,AH=DH÷tan∠DAH=8÷tan45°=8(米),
在Rt△FGE中,i=1:2= ,
,
∴FG=2EG=16(米),
∴AF=FG+GH-AH=16+2-8=10(米);
(2)加宽部分的体积V=S梯形AFED×坝长= ×(2+10)×8×400=19200(立方米).
×(2+10)×8×400=19200(立方米).
答:(1)加固后坝底增加的宽度AF为10米;(2)完成这项工程需要土石19200立方米.
分析:(1)分别过E、D作AB的垂线,设垂足为G、H.在Rt△EFG中,根据坡面的铅直高度(即坝高)及坡比,即可求出FG的长,同理可在Rt△ADH中求出AH的长;由AF=FG+GH-AH求出AF的长.
(2)已知了梯形AFED的上下底和高,易求得其面积.梯形AFED的面积乘以坝长即为所需的土石的体积.
点评:本题考查了解直角三角形的应用,解答本题的关键是理解坡度、坡比的含义,构造直角三角形,利用三角函数表示相关线段的长度,难度一般.

∵四边形ABCD是梯形,且AB∥CD,
∴DH平行且等于EG,
故四边形EGHD是矩形,
∴ED=GH,
在Rt△ADH中,AH=DH÷tan∠DAH=8÷tan45°=8(米),
在Rt△FGE中,i=1:2=
 ,
,∴FG=2EG=16(米),
∴AF=FG+GH-AH=16+2-8=10(米);
(2)加宽部分的体积V=S梯形AFED×坝长=
 ×(2+10)×8×400=19200(立方米).
×(2+10)×8×400=19200(立方米).答:(1)加固后坝底增加的宽度AF为10米;(2)完成这项工程需要土石19200立方米.
分析:(1)分别过E、D作AB的垂线,设垂足为G、H.在Rt△EFG中,根据坡面的铅直高度(即坝高)及坡比,即可求出FG的长,同理可在Rt△ADH中求出AH的长;由AF=FG+GH-AH求出AF的长.
(2)已知了梯形AFED的上下底和高,易求得其面积.梯形AFED的面积乘以坝长即为所需的土石的体积.
点评:本题考查了解直角三角形的应用,解答本题的关键是理解坡度、坡比的含义,构造直角三角形,利用三角函数表示相关线段的长度,难度一般.

练习册系列答案
相关题目
 时,求x值.
时,求x值. 如图是一个由多个相同的小正方形堆积而成的几何体,从上面看得到平面图形,小正方形中的数字表示在该位置的小正方体的个数,请你画出该几何体从正面看到和从左面看到所得的平面图形.
如图是一个由多个相同的小正方形堆积而成的几何体,从上面看得到平面图形,小正方形中的数字表示在该位置的小正方体的个数,请你画出该几何体从正面看到和从左面看到所得的平面图形.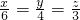 (x、y、z均不为零),则
(x、y、z均不为零),则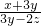 =________.
=________. ,
, B、2-(
B、2-( +m)C、m-1 D、1-
+m)C、m-1 D、1-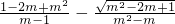 .
. 如图是由五个相同的小立方块搭成的几何体,这个几何体的主视图是
如图是由五个相同的小立方块搭成的几何体,这个几何体的主视图是



 如图,张大爷要围成一个矩形ABCD花圃.花圃的一边AD利用足够长的墙,另三边恰好用总长为36米的篱笆围成.设AB的长为x米,矩形ABCD的面积为S平方米.
如图,张大爷要围成一个矩形ABCD花圃.花圃的一边AD利用足够长的墙,另三边恰好用总长为36米的篱笆围成.设AB的长为x米,矩形ABCD的面积为S平方米.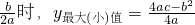 ].
].