题目内容
(2001•陕西)已知△ABC内接⊙O.(1)当点O与AB有怎样的位置关系时,∠ACB是直角;
(2)在满足(1)的条件下,过点C作直线交AB于D,当CD与AB有什么样的关系时,△ABC∽△CBD∽△ACD
(3)画出符合(1)(2)题意的两种图形,使图形中的CD=2cm.
【答案】分析:(1)要保证∠ACB是直角,根据直径所对的圆周角是直角,则AB应是直径,即点O在AB上;
(2)若要这三个三角形相似,则需要∠ABC=∠ACD,则可以得到CD应垂直于AB;
(3)根据射影定理,则CD=2,得AD•BD=4,所以可以让AD=3,BD=1.
解答:解:(1)若要使∠ACB=90°,
则根据90°的圆周角所对的弦是直径,
可得AB应是直径,
即点O应在AB上;
(2)若要△ABC∽△CBD∽△ACD,
则∠ABC=∠ACD.
又∠ACD+∠BCD=90°,
∴∠B+∠BCD=90°.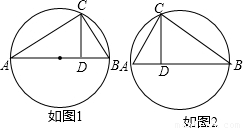
则CD⊥AB.
(3)根据上述结论,可以让AD=3,BD=1或AD=1,BD=3(如图1和2).
点评:考查了圆周角定理的推论,掌握相似三角形的性质.能够根据要满足的结论分析应满足的条件.
(2)若要这三个三角形相似,则需要∠ABC=∠ACD,则可以得到CD应垂直于AB;
(3)根据射影定理,则CD=2,得AD•BD=4,所以可以让AD=3,BD=1.
解答:解:(1)若要使∠ACB=90°,
则根据90°的圆周角所对的弦是直径,
可得AB应是直径,
即点O应在AB上;
(2)若要△ABC∽△CBD∽△ACD,
则∠ABC=∠ACD.
又∠ACD+∠BCD=90°,
∴∠B+∠BCD=90°.

则CD⊥AB.
(3)根据上述结论,可以让AD=3,BD=1或AD=1,BD=3(如图1和2).
点评:考查了圆周角定理的推论,掌握相似三角形的性质.能够根据要满足的结论分析应满足的条件.

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
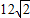 cm,那么这个直角三角形外接圆的半径是 cm.
cm,那么这个直角三角形外接圆的半径是 cm. cm,那么这个直角三角形外接圆的半径是 cm.
cm,那么这个直角三角形外接圆的半径是 cm.