题目内容
已知:如图,在直角坐标系中,以点M(1,0)为圆心、直径AC为2| 2 |
(1)求点A的坐标;
(2)设过点A的直线y=x+b与x轴交于点B.探究:直线AB是否⊙M的切线并对你的结论加以证明;
(3)在(2)的前提下,连接BC,记△ABC的外接圆面积为S1、⊙M面积为S2,若
| S1 |
| S2 |
| h |
| 4 |
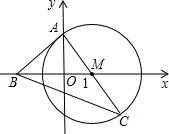 经过B、M两点,且它的顶点到x轴的距离为h.求这条抛物线的解析式.
经过B、M两点,且它的顶点到x轴的距离为h.求这条抛物线的解析式.
分析:(1)在Rt△AOM中根据勾股定理就可以求出OA的长,从而得到点A的坐标;
(2)把A点的坐标代入直线y=x+b的解析式,进而可以求出OA、OB、OM的长度,根据勾股定理可以得到AB、BM、AM的长度,根据勾股定理的逆定理就可以证出△ABM是直角三角形,得到直线AB是⊙M的切线;
(3)△ABC是直角三角形,BC是斜边,即外接圆的直径.在直角△ABC中,根据勾股定理就可以求出BC的长,就可以求出△ABC的外接圆面积S1.⊙M面积为S2容易得到.根据
=
就可以求出h的值,则得到抛物线的顶点的纵坐标,再根据y=ax2+bx+c经过B、M两点,利用待定系数法就可以求出函数的解析式.
(2)把A点的坐标代入直线y=x+b的解析式,进而可以求出OA、OB、OM的长度,根据勾股定理可以得到AB、BM、AM的长度,根据勾股定理的逆定理就可以证出△ABM是直角三角形,得到直线AB是⊙M的切线;
(3)△ABC是直角三角形,BC是斜边,即外接圆的直径.在直角△ABC中,根据勾股定理就可以求出BC的长,就可以求出△ABC的外接圆面积S1.⊙M面积为S2容易得到.根据
| S1 |
| S2 |
| h |
| 4 |
解答:解:(1)由已知AM=
,OM=1,(1分)
在Rt△AOM中,AO=
=1,(2分)
∴点A的坐标为A(0,1)(3分)
(2)证法一:∵直线y=x+b过点A(0,1)
∴1=0+b,即b=1,
∴y=x+1,
令y=0,则x=-1,
∴B(-1,0),(4分)
AB=
=
=
在△ABM中,∵AB=
,AM=
,BM=2.
AB2+AM2=(
)2+(
)2=4=BM2(5分)
∴△ABM是直角三角形,∠BAM=90°,
∴直线AB是⊙M的切线.(6分)
证法二:由证法一得B(-1,0),(4分)
∵AO=BO=OM=1,AO⊥BM,
∴∠BAM=∠1+∠2=45°+45°=90°(5分)
∴直线AB是⊙M的切线.(6分)
(3)解法一:由(2)得∠BAC=90°,AB=
,AC=2
∴BC=
=
=
∵∠BAC=90°,
∴△ABC的外接圆的直径为BC,
∴S1=(
)2•π=(
)2•π=
π(7分)
而S2=(
)2•π=(
)2•π=2π
∵
=
,即
=
,
∴h=5(8分)
设经过点B(-1,0)、M(1、0)的抛物线的解析式为:y=a(x+1)(x-1),(a≠0)即y=ax2-a,
∴-a=±5,
∴a=±5,
∴抛物线解析式为y=5x2-5或y=-5x2+5.(9分)
解法二:(接上)求得
∴h=5(8分)
由已知所求抛物线经过点B(-1,0)、M(1、0),则抛物线的对称轴是y轴,
由题意得抛物线的顶点坐标为(0,±5)
∴抛物线解析式可设为y=a(x-0)2±5
∴B(-1,0)、M(1,0)在抛物线上,
∴a±5=0
∴a=?5
∴抛物线解析式为y=5x2-5或y=-5x2+5.(9分)
解法三:(接上)求得∴h=5(8分)
因为抛物线的方程为y=ax2+bx+(a≠0),由已知得
解得
或
∴抛物线解析式为y=5x2-5或y=-5x2+5.(9分)
| 2 |
在Rt△AOM中,AO=
| AM2-OM2 |
∴点A的坐标为A(0,1)(3分)
(2)证法一:∵直线y=x+b过点A(0,1)
∴1=0+b,即b=1,
∴y=x+1,
令y=0,则x=-1,
∴B(-1,0),(4分)
AB=
| BO2+AO2 |
| 12+12 |
| 2 |
在△ABM中,∵AB=
| 2 |
| 2 |
AB2+AM2=(
| 2 |
| 2 |
∴△ABM是直角三角形,∠BAM=90°,
∴直线AB是⊙M的切线.(6分)
证法二:由证法一得B(-1,0),(4分)
∵AO=BO=OM=1,AO⊥BM,
∴∠BAM=∠1+∠2=45°+45°=90°(5分)
∴直线AB是⊙M的切线.(6分)
(3)解法一:由(2)得∠BAC=90°,AB=
| 2 |
| 2 |
∴BC=
| AB2+AC2 |
(
|
| 10 |
∵∠BAC=90°,
∴△ABC的外接圆的直径为BC,
∴S1=(
| BC |
| 2 |
| ||
| 2 |
| 5 |
| 2 |
而S2=(
| AC |
| 2 |
2
| ||
| 2 |
∵
| S1 |
| S2 |
| h |
| 4 |
| ||
| 2π |
| h |
| 4 |
∴h=5(8分)
设经过点B(-1,0)、M(1、0)的抛物线的解析式为:y=a(x+1)(x-1),(a≠0)即y=ax2-a,
∴-a=±5,
∴a=±5,
∴抛物线解析式为y=5x2-5或y=-5x2+5.(9分)
解法二:(接上)求得
∴h=5(8分)
由已知所求抛物线经过点B(-1,0)、M(1、0),则抛物线的对称轴是y轴,
由题意得抛物线的顶点坐标为(0,±5)
∴抛物线解析式可设为y=a(x-0)2±5
∴B(-1,0)、M(1,0)在抛物线上,
∴a±5=0
∴a=?5
∴抛物线解析式为y=5x2-5或y=-5x2+5.(9分)
解法三:(接上)求得∴h=5(8分)
因为抛物线的方程为y=ax2+bx+(a≠0),由已知得
|
解得
|
|
∴抛物线解析式为y=5x2-5或y=-5x2+5.(9分)
点评:本题主要考查了切线的证明方法,以及待定系数法求函数解析式,计算量较大.

练习册系列答案
相关题目

 的图象的一个分支位于第一象限.
的图象的一个分支位于第一象限.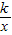 的图象的图象上,求k的值;
的图象的图象上,求k的值; S1?
S1?
 的图象与y轴交于点A,
的图象与y轴交于点A, 的图象分别交于点M,N,已知△AOB的面积为1,点M的纵坐
的图象分别交于点M,N,已知△AOB的面积为1,点M的纵坐 时x的取值范围。
时x的取值范围。
 中,四边形OABC是矩形,点A,C的坐
中,四边形OABC是矩形,点A,C的坐 =-
=- +
+ 交折线O-A-B于点E.
交折线O-A-B于点E.
