题目内容
【题目】已知a、b是正实数,那么, ![]() 是恒成立的.
是恒成立的. 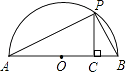
(1)由 ![]() 恒成立,说明
恒成立,说明 ![]() 恒成立;
恒成立;
(2)已知a、b、c是正实数,由 ![]() 恒成立,猜测:
恒成立,猜测: ![]()
![]() 也恒成立;
也恒成立;
(3)如图,已知AB是直径,点P是弧上异于点A和点B的一点,PC⊥AB,垂足为C,AC=a,BC=b,由此图说明 ![]() 恒成立.
恒成立.
【答案】
(1)解:∵( ![]() )2≥0,
)2≥0,
∴a﹣2 ![]() +b≥0,
+b≥0,
∴a+b≥2 ![]() ,
,
∴ ![]() ≥
≥ ![]()
(2)解: ![]() ;
;
理由:a3+b3+c3﹣3abc
=(a+b+c)(a2+b2+c2﹣ab﹣bc﹣ac)
= ![]() (a+b+c)(2a2+2b2+2c2﹣2ab﹣2bc﹣2ac)
(a+b+c)(2a2+2b2+2c2﹣2ab﹣2bc﹣2ac)
= ![]() (a+b+c)[(a﹣b)2+(b﹣c)2+(c﹣a)2]
(a+b+c)[(a﹣b)2+(b﹣c)2+(c﹣a)2]
∵a、b、c是正实数,
∴a3+b3+c3﹣3abc≥0,
∴a3+b3+c3≥3abc,
同理: ![]()
![]() 也恒成立;
也恒成立;
故答案为: ![]()
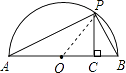
(3)解:如图,连接OP,
∵AB是直径,
∴∠APB=90°,
又∵PC⊥AB,
∴∠ACP=∠APB=90°,
∴∠A+∠B=∠A+∠APC=90°,
∴∠APC=∠B,
∴Rt△APC∽Rt△PBC,
∴ ![]() ,
,
∴PC2=ACCB=ab,
∴PC= ![]() ,
,
又∵PO= ![]() ,
,
∵PO≥PC,
∴ ![]() .
.
【解析】(1)由( ![]() )2≥0,利用完全平方公式,即可证得
)2≥0,利用完全平方公式,即可证得 ![]() 恒成立;(2)由a3+b3+c3﹣3abc=(a+b+c)(a2+b2+c2﹣ab﹣bc﹣ac)=
恒成立;(2)由a3+b3+c3﹣3abc=(a+b+c)(a2+b2+c2﹣ab﹣bc﹣ac)= ![]() (a+b+c)[(a﹣b)2+(b﹣c)2+(c﹣a)2],可证得a3+b3+c3≥3abc,即可得
(a+b+c)[(a﹣b)2+(b﹣c)2+(c﹣a)2],可证得a3+b3+c3≥3abc,即可得 ![]()
![]() 也恒立;(3)首先证得Rt△APC∽Rt△PBC,由相似三角形的对应边成比例,可求得PC的值,又由OP是半径,可求得OP=
也恒立;(3)首先证得Rt△APC∽Rt△PBC,由相似三角形的对应边成比例,可求得PC的值,又由OP是半径,可求得OP= ![]() ,然后由点到线的距离垂线段最短,即可证得
,然后由点到线的距离垂线段最短,即可证得 ![]() 恒成立.
恒成立.
【考点精析】通过灵活运用圆周角定理和相似三角形的判定与性质,掌握顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方即可以解答此题.

【题目】列方程组解应用题:
为了保护环境,深圳某公交公司决定购买一批共10台全新的混合动力公交车,现有A、B两种型号,其中每台的价格,年省油量如下表:
A | B | |
价格(万元/台) | a | b |
节省的油量(万升/年) | 2.4 | 2 |
经调查,购买一台A型车比购买一台B型车多20万元,购买2台A型车比购买3台B型车少60万元.
(1)请求出a和b;
(2)若购买这批混合动力公交车每年能节省22.4万汽油,求购买这批混合动力公交车需要多少万元?