题目内容
如下图，在边长为3的正方形ABCD中，圆O1与圆O2外切，且圆O1分别与DA、DC边相切，圆O2分别与BA、BC边相切，则圆心距O1O2为 .
【答案】
。
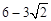【解析】连接BD，则圆心O1、O2在BD上，设⊙P与正方形的切点为H、G，
设圆O1的半径为R，圆O2的半径为r，
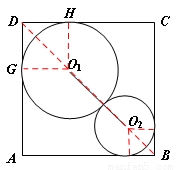
∵且O1分别与DA、DC边相切，∴O1G⊥AD、O1H⊥DC。
又∵O1G= O1H=R，∴四边形GO1HD为正方形。
∴
。
同理，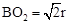
。
∵AB=AD=3cm，∴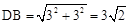
。
∴DO1+ O1O2+BO2=BD=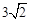
，即：
。
∴
。
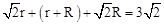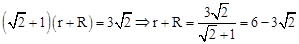∴圆心距O1O2为。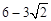
练习册系列答案
相关题目
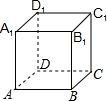如下图，在边长为1的正方体ABCD-A1B1C1D1表面上，一只蚂蚁从A点出发爬到C1点，则蚂蚁爬行的最短路程为（ ）A、
| ||
| B、3 | ||
| C、2 | ||
D、
|
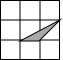
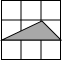
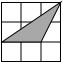
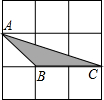
如下图，在边长为1的正方形网格中，点A、B、C均在格点上．则下列四个图形中的三角形（阴影部分，顶点均在格点上）与△ABC相似的是（ ）
