题目内容
某学校准备从甲、乙、丙三位同学中选拔一人参加全市射击比赛,他们在选拔比赛中,射靶十次的平均环数是 =8.1,方差分别是s2甲=1.3,s2乙=2.6,s2丙=3.0,那么根据以上提供的信息,你认为应该推荐参加全市射击比赛的同学是 .
=8.1,方差分别是s2甲=1.3,s2乙=2.6,s2丙=3.0,那么根据以上提供的信息,你认为应该推荐参加全市射击比赛的同学是 .
【答案】分析:根据方差的意义,比较三人方差大小即可.
解答:解:由题意知,s2甲<s2乙<s2丙,而方差反映了一组数据的波动大小,方差越大,波动性越大,反之也成立,
∴应该推荐参加全市射击比赛的同学是甲.
故填甲.
点评:本题考查方差的定义与意义:一般地设n个数据,x1,x2,…xn的平均数为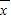 ,则方差S2=
,则方差S2=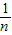 [(x1-
[(x1-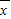 )2+(x2-
)2+(x2-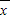 )2+…+(xn-
)2+…+(xn- )2],它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.
)2],它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.
解答:解:由题意知,s2甲<s2乙<s2丙,而方差反映了一组数据的波动大小,方差越大,波动性越大,反之也成立,
∴应该推荐参加全市射击比赛的同学是甲.
故填甲.
点评:本题考查方差的定义与意义:一般地设n个数据,x1,x2,…xn的平均数为
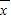 ,则方差S2=
,则方差S2=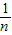 [(x1-
[(x1-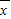 )2+(x2-
)2+(x2-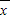 )2+…+(xn-
)2+…+(xn- )2],它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.
)2],它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立. 
练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
某学校准备从甲、乙、丙、丁四位学生中选出一名学生做学生会干部,对四位学生进行了德、智、体、美、劳的综合测试,四人成绩如下表.同时又请100位同学对四位同学做推荐选举投票,投票结果如扇形统计图所示,学校决定综合测试成绩与民主推荐的分数比是6:4,即:综合测试成绩的60%和民主推荐成绩的40%计入总成绩.最后分数最高的当选为学生会干部.请你完成下列问题:
(1)已知四人综合测试成绩的平均分是72分,请你通过计算补全表格中的数据;
(2)参加推荐选举投票的100人中,推荐丁的有______人;
(3)按要求应该由哪位同学担任学生会干部职务,请你计算出他的最后得分.

| 参加测试人员 | 甲 | 乙 | 丙 | 丁 |
| 综合测试成绩 | 74 | 73 | 66 | 75 |
(2)参加推荐选举投票的100人中,推荐丁的有______人;
(3)按要求应该由哪位同学担任学生会干部职务,请你计算出他的最后得分.

某学校准备从甲、乙、丙、丁四位学生中选出一名学生做学生会干部,对四位学生进行了德、智、体、美、劳的综合测试,四人成绩如下表.同时又请100位同学对四位同学做推荐选举投票,投票结果如扇形统计图所示,学校决定综合测试成绩与民主推荐的分数比是6:4,即:综合测试成绩的60%和民主推荐成绩的40%计入总成绩.最后分数最高的当选为学生会干部.请你完成下列问题:
(1)已知四人综合测试成绩的平均分是72分,请你通过计算补全表格中的数据;
(2)参加推荐选举投票的100人中,推荐丁的有______人;
(3)按要求应该由哪位同学担任学生会干部职务,请你计算出他的最后得分.

| 参加测试人员 | 甲 | 乙 | 丙 | 丁 |
| 综合测试成绩 | 74 | 73 | 66 | 75 |
(2)参加推荐选举投票的100人中,推荐丁的有______人;
(3)按要求应该由哪位同学担任学生会干部职务,请你计算出他的最后得分.

 19、某学校准备从甲、乙、丙、丁四位学生中选出一名学生做学生会干部,对四位学生进行了德、智、体、美、劳的综合测试,四人成绩如下表.同时又请100位同学对四位同学做推荐选举投票,投票结果如扇形统计图所示,学校决定综合测试成绩与民主推荐的分数比是6:4,即:综合测试成绩的60%和民主推荐成绩的40%计入总成绩.最后分数最高的当选为学生会干部.请你完成下列问题:
19、某学校准备从甲、乙、丙、丁四位学生中选出一名学生做学生会干部,对四位学生进行了德、智、体、美、劳的综合测试,四人成绩如下表.同时又请100位同学对四位同学做推荐选举投票,投票结果如扇形统计图所示,学校决定综合测试成绩与民主推荐的分数比是6:4,即:综合测试成绩的60%和民主推荐成绩的40%计入总成绩.最后分数最高的当选为学生会干部.请你完成下列问题: