题目内容
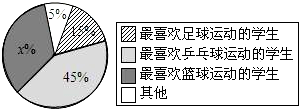
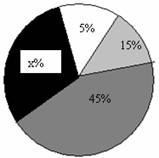
某校一课外活动小组为了解学生最喜欢的球类运动情况,随机抽查本校九年级的200名学生,调查的结果如图所示.请根据该扇形统计图解答以下问题:
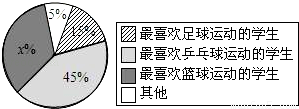
(1)求图中的x的值;
(2)求最喜欢乒乓球运动的学生人数;
(3)若由3名最喜欢篮球运动的学生,1名最喜欢乒乓球运动的学生,1名最喜欢足球运动的学生组队外出参加一次联谊活动.欲从中选出2人担任组长(不分正副),列出所有可能情况,并求2人均是最喜欢篮球运动的学生的概率.
【答案】
解:(1)由题得:x%+5%+15%+45%=1,解得:x=35。
(2)最喜欢乒乓球运动的学生人数为200×45%=90(人)。
(3)用A1,A2,A3表示3名最喜欢篮球运动的学生,B表示1名最喜欢乒乓球运动的学生,C表示1名喜欢足球运动的学生,则从5人中选出2人的情况有:(A1,A2),(A1,A3),(A1,B),(A1,C),(A2,A3),(A2,B),(A2,C),(A3,B),(A3,C),(B,C),共计10种,
选出的2人都是最喜欢篮球运动的学生的有(A1,A2),(A1,A3),(A2,A3)共计3种,
∴选出2人都最喜欢篮球运动的学生的概率为 。
。
【解析】
试题分析:(1)考查了扇形图的性质,注意所有小扇形的百分数和为1。
(2)根据扇形图求解,解题的关键是找到对应量:最喜欢乒乓球运动的学生人数对应的百分比为x%。
(3)此题可以采用列举法,注意要做到不重不漏。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目