题目内容
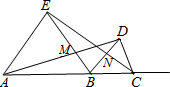 如图,在△ABE和△BCD中,AB=BE=EA,BC=CD=DB,且两个三角形在线段AC同侧,则下列式子中错误的是
如图,在△ABE和△BCD中,AB=BE=EA,BC=CD=DB,且两个三角形在线段AC同侧,则下列式子中错误的是
- A.△ABD≌△EBC
- B.△NBC≌△MBD
- C.△ABM≌△EBN
- D.△ABE≌△BCD
D
分析:根据等边三角形的性质,即可推出△ABD≌△EBC,可得∠BDM=∠BCN,∠BEN=∠BAM,即可推出△NBC≌△MBD,然后可得BM=BN,即可推出△ABM≌△EBN.
解答:∵AB=BE=EA,BC=CD=DB,
∴△ABE和△BCD为等边三角形,
∴∠ABE=∠DBC=∠DCB=∠EBD=60°,
∴∠ABD=∠EBC=120°,
∵在△ABD和△EBC中,
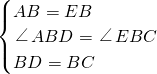 ,
,
∴△ABD和△EBC(SAS),
∴∠ADB=∠ECB,
∵在△NBC和△MBD中,
 ,
,
∴△NBC≌△MBD(AAS),
∴BM=BN,
∵在△ABM和△EBN中,
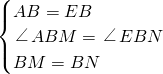 ,
,
∴△ABM≌△EBN(SAS).
故选D.
点评:本题主要考查等边三角形的性质、全等三角形的判定与性质,关键在于根据相关的性质和判定定理推出相关的三角形全等.
分析:根据等边三角形的性质,即可推出△ABD≌△EBC,可得∠BDM=∠BCN,∠BEN=∠BAM,即可推出△NBC≌△MBD,然后可得BM=BN,即可推出△ABM≌△EBN.
解答:∵AB=BE=EA,BC=CD=DB,
∴△ABE和△BCD为等边三角形,
∴∠ABE=∠DBC=∠DCB=∠EBD=60°,
∴∠ABD=∠EBC=120°,
∵在△ABD和△EBC中,
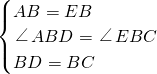 ,
,∴△ABD和△EBC(SAS),
∴∠ADB=∠ECB,
∵在△NBC和△MBD中,
 ,
,∴△NBC≌△MBD(AAS),
∴BM=BN,
∵在△ABM和△EBN中,
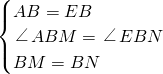 ,
,∴△ABM≌△EBN(SAS).
故选D.
点评:本题主要考查等边三角形的性质、全等三角形的判定与性质,关键在于根据相关的性质和判定定理推出相关的三角形全等.

练习册系列答案
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案
相关题目
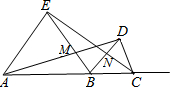 如图,在△ABE和△BCD中,AB=BE=EA,BC=CD=DB,且两个三角形在线段AC同侧,则下列式子中错误的是( )
如图,在△ABE和△BCD中,AB=BE=EA,BC=CD=DB,且两个三角形在线段AC同侧,则下列式子中错误的是( )| A、△ABD≌△EBC | B、△NBC≌△MBD | C、△ABM≌△EBN | D、△ABE≌△BCD |
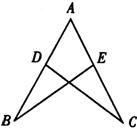 14、如图,在△ABE和△ACD中,AE=AD,添加一个条件
14、如图,在△ABE和△ACD中,AE=AD,添加一个条件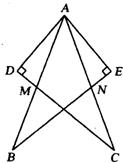 2、如图,在△ABE和△ACD中,给出以下四个论断:
2、如图,在△ABE和△ACD中,给出以下四个论断: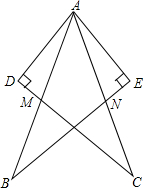 如图,在△ABE和△ACD中,给出以下四个论断:①AB=AC;②AD=AE;③AM=AN;④AD⊥DC,AE⊥BE.以其中三个论断为题设,填入下面的“已知”栏中,一个论断为结论,填入下面的“求证”栏中,使其组成一个正确的命题.
如图,在△ABE和△ACD中,给出以下四个论断:①AB=AC;②AD=AE;③AM=AN;④AD⊥DC,AE⊥BE.以其中三个论断为题设,填入下面的“已知”栏中,一个论断为结论,填入下面的“求证”栏中,使其组成一个正确的命题.