题目内容
为了预防春季流感，尤其是对H7N9禽流感的防控，学校计划利用周末将教室及公共环境进行“药熏消毒”，现有甲、乙两人准备承接该工作，若甲、乙合做6小时可以完成全部工作；若甲单独做4小时后，剩下的乙单独做还需9小时完成．
（1）求甲、乙两人单独完成该工作各需多少小时？
（2）若学校需付给甲每小时工钱30元，付给乙每小时工钱40元，要使完成该工作时支付工钱不超过480元，乙最多工作多少小时？
解：（1）设甲、乙两人单独完成该工作各需x、y小时，
由题意得，
，
解得：
，
经检验他们是原方程的解，
答：甲、乙两人单独完成该工作各需10、15小时；
（2）设甲工作m小时，乙工作n小时完成该工作，
由题意得，
，
解得：n≤9，
答：乙最多工作9小时．
分析：（1）设甲、乙两人单独完成该工作各需x、y小时，则可得出甲的工作效率为
，乙的工作效率为
，根据甲、乙合做6小时可以完成全部工作；若甲单独做4小时后，剩下的乙单独做还需9小时完成，列出方程组，解出即可；
（2）设甲工作m小时，乙工作n小时完成该工作，根据两人要完成工作量可得：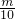
+
=1，再由完成该工作时支付工钱不超过480元，可得出30m+40n≤480，联立求解即可．
点评：本题考查了分式方程的应用，解答本题的关键是设出未知数，表示出甲、乙的工作效率，根据等量关系列出方程．
由题意得，
，解得：
，经检验他们是原方程的解，
答：甲、乙两人单独完成该工作各需10、15小时；
（2）设甲工作m小时，乙工作n小时完成该工作，
由题意得，
，解得：n≤9，
答：乙最多工作9小时．
分析：（1）设甲、乙两人单独完成该工作各需x、y小时，则可得出甲的工作效率为
，乙的工作效率为，根据甲、乙合做6小时可以完成全部工作；若甲单独做4小时后，剩下的乙单独做还需9小时完成，列出方程组，解出即可；（2）设甲工作m小时，乙工作n小时完成该工作，根据两人要完成工作量可得：
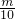+=1，再由完成该工作时支付工钱不超过480元，可得出30m+40n≤480，联立求解即可．点评：本题考查了分式方程的应用，解答本题的关键是设出未知数，表示出甲、乙的工作效率，根据等量关系列出方程．
练习册系列答案
一线名师提优试卷系列答案
相关题目
