题目内容
如图所示,AE=AC,∠E=∠C=100°,ED=CB,∠D=35°,∠CAD=10°,求∠BAE的度数.

分析:根据三角形内角和定理可求∠EAD的度数,由角的和差关系得到∠EAC的度数,根据SAS可证△AED≌△ACD,根据全等三角形的性质得到∠CAB的度数,从而求得∠BAE的度数.
解答:解:∵∠E=100°,∠D=35°,
∴∠EAD=45°,
∵∠CAD=10°,
∴∠EAC=35°,
∵在△AED与△ACD中,
∴△AED≌△ACD(SAS),
∴∠CAB=∠EAD=45°,
∴∠BAE=35°+45°=80°.
∴∠EAD=45°,
∵∠CAD=10°,
∴∠EAC=35°,
∵在△AED与△ACD中,
|
∴△AED≌△ACD(SAS),
∴∠CAB=∠EAD=45°,
∴∠BAE=35°+45°=80°.
点评:考查了三角形内角和定理,全等三角形的判定与性质,以及角的和差关系,解题的关键是证明△AED≌△ACD.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
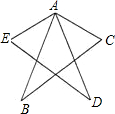 如图所示,AE=AC,AB=AD,∠EAB=∠CAD.求证:∠B=∠D.
如图所示,AE=AC,AB=AD,∠EAB=∠CAD.求证:∠B=∠D. 3、如图所示,AE、BD相交于点C,要使△ABC≌△EDC,至少要添加的条件是
3、如图所示,AE、BD相交于点C,要使△ABC≌△EDC,至少要添加的条件是
 如图所示,AE=AC,AB=AD,∠EAB=∠CAD.求证:∠B=∠D.
如图所示,AE=AC,AB=AD,∠EAB=∠CAD.求证:∠B=∠D.