题目内容
如图是用橡皮筋在格点中围成的五个图形,图形内部的格点,称为内格点;图形边界上的格点称为外格点.(每个最小格点正方形的边长为一个单位,以下同)
(1)请统计图1中每个图形内格点数L、外格点数N,计算出这些图形的面积S,并完成下表:
| 图形 | 内格点数L | 外格点数的一半N | 面积S |
| A | 1.5 | 0.5 | |
| B | 1 | 4 | 4 |
| C | 3 | ______ | ______ |
| D | 3 | ______ | ______ |
| E | 4 | ______ | ______ |
(3)运用上述关系式,计算图(2)中格点图形F的面积.
【答案】分析:(1)根据图形确定答案即可;
(2)分两种情况得到S与L的关系式即可;
(3)将L=10,N=12时代入上题求得的关系式即可求解.
解答:解:(1)如图所示:
(2)根据C、D,当L不变时,S-L=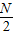 -1;根据A、B、E,当N不变时,S-
-1;根据A、B、E,当N不变时,S-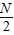 =L-1;
=L-1;
综上,得:S=L+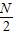 -1;
-1;
(3)当L=10,N=12时,S=10+6-1=15
点评:本题考查了图形的变化类问题,解题的关键是从图形中得到相关数据,并从这些数据中得到关系式.
(2)分两种情况得到S与L的关系式即可;
(3)将L=10,N=12时代入上题求得的关系式即可求解.
解答:解:(1)如图所示:
| 图形 | 内格点数L | 外格点数的一半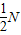 | 面积S |
| A | 1.5 | 0.5 | |
| B | 1 | 4 | 4 |
| C | 3 | 4 | 6 |
| D | 3 | 6 | 8 |
| E | 4 | 4 | 7 |
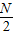 -1;根据A、B、E,当N不变时,S-
-1;根据A、B、E,当N不变时,S-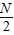 =L-1;
=L-1;综上,得:S=L+
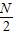 -1;
-1;(3)当L=10,N=12时,S=10+6-1=15
点评:本题考查了图形的变化类问题,解题的关键是从图形中得到相关数据,并从这些数据中得到关系式.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
如图是用橡皮筋在格点中围成的五个图形,图形内部的格点,称为内格点;图形边界上的格点称为外格点.(每个最小格点正方形的边长为一个单位,以下同)

(1)请统计图1中每个图形内格点数L、外格点数N,计算出这些图形的面积S,并完成下表:
| 图形 | 内格点数L | 外格点数的一半N | 面积S |
| A | 0 | 1.5 | 0.5 |
| B | 1 | 4 | 4 |
| C | 3 | ________ | ________ |
| D | 3 | ________ | ________ |
| E | 4 | ________ | ________ |
(3)运用上述关系式,计算图(2)中格点图形F的面积.
