题目内容
12、设m是不能表示为三个互不相等的合数之和的最大整数，则m=
17
分析：最小三个合数的和是18，因而17是满足条件的数，若m＞18，可以分m是奇数和偶数两种情况证明不满足题意．
解答：解：最小三个合数是4，6，8，4+6+8=18，故17是不能表示为三个互不相等的合数之和的整数，
当m＞18时，若m=2k＞18，则m=4+6+2（k-5），
若m=2k-1＞18，则m=4+9+2（k-7）即任意大于18的整数均可表示为三个互不相等的合数之和，
故m=17．
故答案是：17．
当m＞18时，若m=2k＞18，则m=4+6+2（k-5），
若m=2k-1＞18，则m=4+9+2（k-7）即任意大于18的整数均可表示为三个互不相等的合数之和，
故m=17．
故答案是：17．
点评：本题主要考查了质数与合数的性质，正确证明m＞18的整数都可以表示成三个互不相等的合数的和是解题的关键．
练习册系列答案
相关题目
，请说明理由．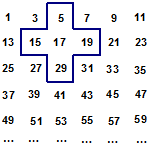
将连续的奇数1，3，5，7，…，排成如图所示的数表，用十字框任意框出5个数．