Question

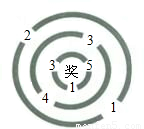
如图，某学校九年级数学兴趣小组组织一次数学活动．在一座有三道环形路的数字迷宫的每个进口处都标记着一个数，要求进入者把自己当做数“1”，进入时必须乘进口处的数，并将结果带到下一个进口，依次累乘下去，在通过最后一个进口时，只有乘积是3的倍数，才可以进入迷宫中心，现让小军从最外环任一个进口进入．
（1）小军能进入迷宫中心的概率是多少？请画出树状图进行说明．
（2）小组两位组员小张和小李商量做一个小游戏，以猜测小军进迷宫的结果比胜负．游戏规则规下：小军如能进入迷宫中心，小张得1分；小军如不能进入迷宫中心，则小李得2分．你认为这个游戏公平吗？请说明理由．

Answer 1

分析：（1）首先根据题意画树状图，然后根据树状图求得所有等可能的结果与小军能进入迷宫中心情况，再根据概率公式求解即可；
（2）首先分别求得小军能进入迷宫中心的概率与小军不能进入迷宫中心的概率，然后求得其得分，比较得分情况即可求得答案．

解答：解：（1）画树状图得：

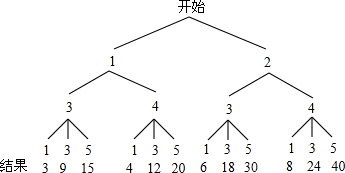
∴一共有12种等可能的结果，
小军能进入迷宫中心的有8种情况，
∴小军能进入迷宫中心的概率是：

8

12

=

2

3

；

（2）公平，理由如下：
由树状图可知，小军能进入迷宫中心的概率是：

8

12

=

2

3

，
小军不能进入迷宫中心的概率是：

1

3

；
小张得分为：1×

2

3

=

2

3

（分），
小李得分为：2×

1

3

=

2

3

（分），
∴公平．

点评：此题考查了树状图法与列表法求概率．树状图法与列表法可以不重不漏的表示出所有等可能的结果．注意游戏公平与否，看其得分即可，相等公平，否则不公平．用到的知识点为：概率=所求情况数与总情况数之比．