题目内容
(2009•瓯海区一模)如图,抛物线y=ax2+bx+c交坐标轴于点A(-1,0)、B(3,0)、C(0,-3).(1)求此抛物线函数解析式及顶点M的坐标;
(2)若直线CM与x轴交于点D,E是C关于此抛物线对称轴的对称点,试判断四边形ADCE的形状并说明理由;
(3)若P是该抛物线上异于A、B两点的一个动点,连接BP交y轴正半轴于点N,是否存在点P使△AOC与△BON相似?若存在请直接写出点P的坐标,若不存在请说明理由.

【答案】分析:(1)将A、B、C三点坐标代入解方程组可得a,b,c的值和抛物线解析式,用顶点坐标公式求顶点坐标;(2)已知点C(0,-3),M(1,-4),根据“两点法”可求直线CM函数解析式及D点坐标,∵E是C关于此抛物线对称轴的对称点,∴点E(2,-3),这样就已知A,D,C,E四点坐标,只要判断线段CE、AD平行且相等即可;
(3)设N(0,n),n>0,△AOC与△BON都是直角三角形要求相似,存在两种对应关系:△AOC∽△BON,△AOC∽△NOB,根据相似比可得N点坐标,再求直线BN解析式与抛物线解析式联立可求P点坐标.
解答:解:
(1)把点A(-1,0)、B(3,0)、C(0,-3)代入抛物线y=ax2+bx+c得:

解得: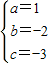
∴抛物线函数解析式为y=x2-2x-3(3分)
顶点M的坐标为(1,-4)(4分)
(2)∵点C(0,-3),M(1,-4)
∴直线CM函数解析式为y=-x-3
∴直线CM与x轴交于点D(-3,0),(6分)
∵E是C关于此抛物线对称轴的对称点,
∴点E(2,-3)
∴CE=AD=2,
又∵CE∥AD
∴四边形ADCE是平行四边形.(8分)
(3)存在点P使△AOC与△BON相似,P1(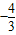 ,
,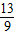 ),P2(-4,21).(12分)
),P2(-4,21).(12分)
点评:本题考查了抛物线解析式及顶点坐标的求法,平行四边形的判断,寻找三角形相似的条件等知识,充分体现形数结合的数学思想.
(3)设N(0,n),n>0,△AOC与△BON都是直角三角形要求相似,存在两种对应关系:△AOC∽△BON,△AOC∽△NOB,根据相似比可得N点坐标,再求直线BN解析式与抛物线解析式联立可求P点坐标.
解答:解:
(1)把点A(-1,0)、B(3,0)、C(0,-3)代入抛物线y=ax2+bx+c得:

解得:
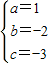
∴抛物线函数解析式为y=x2-2x-3(3分)
顶点M的坐标为(1,-4)(4分)
(2)∵点C(0,-3),M(1,-4)
∴直线CM函数解析式为y=-x-3
∴直线CM与x轴交于点D(-3,0),(6分)
∵E是C关于此抛物线对称轴的对称点,
∴点E(2,-3)
∴CE=AD=2,
又∵CE∥AD
∴四边形ADCE是平行四边形.(8分)
(3)存在点P使△AOC与△BON相似,P1(
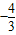 ,
,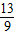 ),P2(-4,21).(12分)
),P2(-4,21).(12分)点评:本题考查了抛物线解析式及顶点坐标的求法,平行四边形的判断,寻找三角形相似的条件等知识,充分体现形数结合的数学思想.

练习册系列答案
相关题目
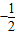

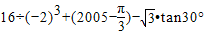 ;
;