Question

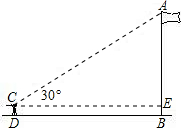
如图，有一位同学用一个含30°角的直角三角板估测学校的旗杆AB的高度，他将30°角的直角边水平放在1.3米高的支架CD上，三角板的斜边与旗杆的顶点在同一直线上，他又量得D、B的距离为15米，则旗杆AB的高度为（≈1.73，结果精确到0.1m）

1. A.
   26.0米
2. B.
   27.3米
3. C.
   8.7米
4. D.
   10.0米

Answer 1

D
分析：本题的关键是求出AE的高度，已知了BD的长度也就是EC的长度，可根据∠ACE=30°，在直角三角形ACE中，用EC的长和∠ACE的正切函数求出AE的长．然后根据旗杆的高度AB=AE+BE即可得出旗杆的长．
解答：在直角三角形ACE中，∠ACE=30°，EC=BD=15（米），
AE=EC•tan∠ACE=215×tan30°=15×≈8.7（米），
因此AB=AE+BE=8.7+1.3=10.0（米）．
即旗杆的高度是10.0米．
故选D．
点评：本题主要考查了解直角三角形的应用，要根据所求和已知的条件正确的选用合适的三角形函数进行求解．