题目内容
 如图,山顶上有一座铁塔,在地面上一点A处测得塔顶B处的仰角α=60°,在山顶C处测得A点的俯角β=45°,已知塔高为50m,则山高CD等于
如图,山顶上有一座铁塔,在地面上一点A处测得塔顶B处的仰角α=60°,在山顶C处测得A点的俯角β=45°,已知塔高为50m,则山高CD等于
- A.25(1+
 )m
)m - B.25(
 -1)m
-1)m - C.25m
- D.(25
 +1)m
+1)m
A
分析:△ACD是等腰直角三角形,CD=AD;在Rt△ADB中选择三角函数表示AD,根据BC=BD-CD得方程求解.
解答:在Rt△ABD中,有BD=AD×tan60°= AD;
AD;
同理可得:DC=AD×tan45°=AD.
∵BC=BD-DC=50,
∴CD=25(1+ )m.
)m.
故选A.
点评:本题考查俯角、仰角的定义,要求学生能借助其关系构造直角三角形并解直角三角形.
分析:△ACD是等腰直角三角形,CD=AD;在Rt△ADB中选择三角函数表示AD,根据BC=BD-CD得方程求解.
解答:在Rt△ABD中,有BD=AD×tan60°=
 AD;
AD;同理可得:DC=AD×tan45°=AD.
∵BC=BD-DC=50,
∴CD=25(1+
 )m.
)m.故选A.
点评:本题考查俯角、仰角的定义,要求学生能借助其关系构造直角三角形并解直角三角形.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
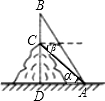 如图,山顶上有一座铁塔,在地面上一点A处测得塔顶B处的仰角α=60°,在山顶C处测得A点的俯角β=45°,已知塔高为50m,则山高CD等于( )
如图,山顶上有一座铁塔,在地面上一点A处测得塔顶B处的仰角α=60°,在山顶C处测得A点的俯角β=45°,已知塔高为50m,则山高CD等于( )A、25(1+
| ||
B、25(
| ||
| C、25m | ||
D、(25
|

 )m
)m -1)m
-1)m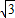 +1)m
+1)m