题目内容
(2005•济宁)如图,点P是x轴上的一点,以P为圆心的圆交x轴于点A(6,0),且与y轴相切于点O,点C(8,0)为x轴上的一点,过点C作⊙P的切线,切点为B.求过B、C两点的直线的解析式.
【答案】分析:因为点A(6,0),C(8,0),利用切割线定理可得CB2=CA•CO=16,即可求出CB=4.利用切线长定理设直线CB交y轴于点D(0,y),则OD=BD=y,再利用勾股定理可得y2+82=(y+4))2,即可求出C(0,6),然后运用待定系数法求解.
解答: 解:∵点A(6,0),C(8,0)
解:∵点A(6,0),C(8,0)
∴OA=6,OC=8,AC=2
∵以⊙P过点A(6,0),且与y轴相切于点O,CB为⊙P的切线,切点为B,
∴CB2=CA•CO=16
∴CB=4
设直线CB交y轴于点D(0,y),则OD=BD=y,
∵∠DOC=90°
∴y2+82=(y+4)2,∴y=6;
∴C(0,6);
设直线BC的解析式为y=kx+b,
∴
∴
∴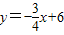 .
.
点评:本题需仔细分析题意,结合图象,利用切线的性质、勾股定理、待定系数法即可解决问题.
解答:
 解:∵点A(6,0),C(8,0)
解:∵点A(6,0),C(8,0)∴OA=6,OC=8,AC=2
∵以⊙P过点A(6,0),且与y轴相切于点O,CB为⊙P的切线,切点为B,
∴CB2=CA•CO=16
∴CB=4
设直线CB交y轴于点D(0,y),则OD=BD=y,
∵∠DOC=90°
∴y2+82=(y+4)2,∴y=6;
∴C(0,6);
设直线BC的解析式为y=kx+b,
∴

∴

∴
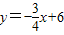 .
.点评:本题需仔细分析题意,结合图象,利用切线的性质、勾股定理、待定系数法即可解决问题.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目



