题目内容
 如图,在等腰梯形ABCD中,AB∥CD,AD=BC=4cm,∠A=60°,BD平分∠ABC,则这个梯形的面积是( )
如图,在等腰梯形ABCD中,AB∥CD,AD=BC=4cm,∠A=60°,BD平分∠ABC,则这个梯形的面积是( )A、6
| ||
B、8
| ||
C、10
| ||
D、12
|
考点:等腰梯形的性质
专题:计算题
分析:过点D作DE⊥AB于E,利用等腰梯形的性质求出DE和AB的长,再利用梯形的面积根据计算即可.
解答:解:过点D作DE⊥AB于E,
∵在等腰梯形ABCD中,AB∥CD,
∴∠A=∠ABC=60°,
∵BD平分∠ABC,
∴∠DBA=30°,
∴∠ADB=90°,
∵AD=BC=4cm,
∴AB=8cm,
∴DB=4
cm,
∴DE=2
cm,
∴这个梯形的面积是=
(4+4)×2
=8
cm2,
故选B.
∵在等腰梯形ABCD中,AB∥CD,

∴∠A=∠ABC=60°,
∵BD平分∠ABC,
∴∠DBA=30°,
∴∠ADB=90°,
∵AD=BC=4cm,
∴AB=8cm,
∴DB=4
| 3 |
∴DE=2
| 3 |
∴这个梯形的面积是=
| 1 |
| 2 |
| 3 |
| 3 |
故选B.
点评:本题考查了等腰梯形的性质,本题涉及到直角三角形的一个定理(直角三角形中30°角所对的直角边等于斜边的一半)以及等腰梯形的性质的运用.

练习册系列答案
相关题目
以下调查中适合作抽样调查的有( )
①了解全班同学期末考试的数学成绩情况;
②了解夏季冷饮市场上冰淇淋的质量情况;
③学校为抗击“非典”,需了解全校师生的体温;
④了解《课课练》在全省七年级学生中受欢迎的程序.
①了解全班同学期末考试的数学成绩情况;
②了解夏季冷饮市场上冰淇淋的质量情况;
③学校为抗击“非典”,需了解全校师生的体温;
④了解《课课练》在全省七年级学生中受欢迎的程序.
| A、1个 | B、2个 | C、3个 | D、4 |
计算x2•x4的结果是( )
| A、x6 |
| B、x7 |
| C、x8 |
| D、x9 |
计算
÷
?
的结果是( )
| -b |
| a2 |
| b2 |
| a2 |
| a2 |
| -b |
A、-
| ||
B、-
| ||
C、
| ||
D、
|
某市有近4万名考生参加中考,为了解这些考生的数学成绩,从中抽取1500名考生的数学成绩进行统计分析,以下说法正确的是( )
| A、这1500名考生是总体的一个样本 |
| B、近4万名考生是总体 |
| C、其中每位考生的数学成绩是个体 |
| D、1500名学生是样本容量 |
下列运算正确的是( )
| A、a2+a3=2a5 |
| B、a8÷a2=a4 |
| C、a-2=-a2 |
| D、(ab)2=a2b2 |
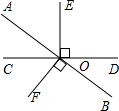 如图,AB与CD交于点O,OE⊥CD,OF⊥AB,∠BOD=25°,则∠AOE=
如图,AB与CD交于点O,OE⊥CD,OF⊥AB,∠BOD=25°,则∠AOE= 如图A、B两点在函数
如图A、B两点在函数