题目内容
如图所示是2008年11月的日历表,
| 星期六 | 星期日 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
(1)若一竖列的三个数的和为42,这三个数分别是多少?若和为44,能求出这三天是几号吗?为什么?
(2)若一竖列的四个数之和为74,这四个数分别是多少?四个数的和能不能是75,为什么?
(3)如果是2×2的矩形块的四个数的和为80,求出这四个数;
(4)如果是3×3的矩形块,九个数的和是171,你能说出这九个数吗?你能发现九个数的和与中间的数的关系吗?为什么?
解:(1)由已知得:设一竖列的三个数依次为:x-7,x,x+7.
则(x-7)+x+(x+7)=42,解之得:x=14,即依次为7,14,21号;
当(x-7)+x+(x+7)=44时,x= ,而x是日期即必须为正整数,
,而x是日期即必须为正整数,
∴和为44,不能求出这三天是几号;
(2)由已知得:设一竖列的四个数依次为:x-7,x,x+7,x+14,
则(x-7)+x+(x+7)+(x+14)=74,
解之得:x=15,
即依次为8,15,22,29号.
当(x-7)+x+(x+7)+(x+14)=75时,x=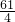 ,而x是日期即必须为正整数.
,而x是日期即必须为正整数.
∴四个数的和不能为75.
(3)设2×2的矩形块的四个数为x,x+1,x+7,x+8,
则x+(x+1)+(x+7)+(x+8)=80,
解之得:x=16,
即依次为16,17,23,24号;
(4)设3×3的矩形块的九个数为x-8,x-7,x-6,x-1,x,x+1,x+6,x+7,x+8,
则(x-8)+(x-7)+(x-6)+(x-1)+x+(x+1)+(x+6)+(x+7)+(x+8)=171,
解之得:x=19,
∴能说出这九个数,他们依次是:11,12,13,18,19,20,25,26,27,
由上可得若设中间数为x,
则(x-8)+(x-7)+(x-6)+(x-1)+x+(x+1)+(x+6)+(x+7)+(x+8)=9x,
∴九个数的和是中间的数的9倍.
分析:(1)关系式为:中间的数-7+中间的数+中间的数+7=42;中间的数-7+中间的数+中间的数+7=44,把相关未知数代入,求得整数解即可;
(2)关系式为:中间的数-7+中间的数+中间的数+7+中间的数+14=74,中间的数-7+中间的数+中间的数+7+中间的数+14=75,把相关未知数代入,求得整数解即可;
(3)可设最小的数为x,那么其余数分别为x+1,x+7,x+8,让这4个数的和为80,列式求值即可;
(4)可设中间的数为x,根据规律设出其余8个数,让它们相加等于171,求解即可;让设出的9个数相加可得和与中间的数的关系.
点评:解决本题的关键是理解日历上每行两个相邻的数相差1,每列2个相邻的数相差7.
则(x-7)+x+(x+7)=42,解之得:x=14,即依次为7,14,21号;
当(x-7)+x+(x+7)=44时,x=
 ,而x是日期即必须为正整数,
,而x是日期即必须为正整数,∴和为44,不能求出这三天是几号;
(2)由已知得:设一竖列的四个数依次为:x-7,x,x+7,x+14,
则(x-7)+x+(x+7)+(x+14)=74,
解之得:x=15,
即依次为8,15,22,29号.
当(x-7)+x+(x+7)+(x+14)=75时,x=
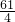 ,而x是日期即必须为正整数.
,而x是日期即必须为正整数.∴四个数的和不能为75.
(3)设2×2的矩形块的四个数为x,x+1,x+7,x+8,
则x+(x+1)+(x+7)+(x+8)=80,
解之得:x=16,
即依次为16,17,23,24号;
(4)设3×3的矩形块的九个数为x-8,x-7,x-6,x-1,x,x+1,x+6,x+7,x+8,
则(x-8)+(x-7)+(x-6)+(x-1)+x+(x+1)+(x+6)+(x+7)+(x+8)=171,
解之得:x=19,
∴能说出这九个数,他们依次是:11,12,13,18,19,20,25,26,27,
由上可得若设中间数为x,
则(x-8)+(x-7)+(x-6)+(x-1)+x+(x+1)+(x+6)+(x+7)+(x+8)=9x,
∴九个数的和是中间的数的9倍.
分析:(1)关系式为:中间的数-7+中间的数+中间的数+7=42;中间的数-7+中间的数+中间的数+7=44,把相关未知数代入,求得整数解即可;
(2)关系式为:中间的数-7+中间的数+中间的数+7+中间的数+14=74,中间的数-7+中间的数+中间的数+7+中间的数+14=75,把相关未知数代入,求得整数解即可;
(3)可设最小的数为x,那么其余数分别为x+1,x+7,x+8,让这4个数的和为80,列式求值即可;
(4)可设中间的数为x,根据规律设出其余8个数,让它们相加等于171,求解即可;让设出的9个数相加可得和与中间的数的关系.
点评:解决本题的关键是理解日历上每行两个相邻的数相差1,每列2个相邻的数相差7.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
如图所示是2008年11月的日历表,
请回答下列问题:
(1)若一竖列的三个数的和为42,这三个数分别是多少?若和为44,能求出这三天是几号吗?为什么?
(2)若一竖列的四个数之和为74,这四个数分别是多少?四个数的和能不能是75,为什么?
(3)如果是2×2的矩形块的四个数的和为80,求出这四个数;
(4)如果是3×3的矩形块,九个数的和是171,你能说出这九个数吗?你能发现九个数的和与中间的数的关系吗?为什么?
| 星期六 | 星期日 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
(1)若一竖列的三个数的和为42,这三个数分别是多少?若和为44,能求出这三天是几号吗?为什么?
(2)若一竖列的四个数之和为74,这四个数分别是多少?四个数的和能不能是75,为什么?
(3)如果是2×2的矩形块的四个数的和为80,求出这四个数;
(4)如果是3×3的矩形块,九个数的和是171,你能说出这九个数吗?你能发现九个数的和与中间的数的关系吗?为什么?

 2008年8月北京成功举办了第29届奥运会,5个城市的国际标准时间(单位:时)在数轴上表示如图所示,那么北京奥运会开幕时间2008年8月8日20时应是( )
2008年8月北京成功举办了第29届奥运会,5个城市的国际标准时间(单位:时)在数轴上表示如图所示,那么北京奥运会开幕时间2008年8月8日20时应是( )