题目内容
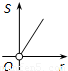
 如图,⊙O的圆心在定角∠α(0°<α<180°)的角平分线上运动,且⊙O与∠α的两边相切,图中阴影部分的面积S关于⊙O的半径r(r>0)变化的函数图象大致是
如图,⊙O的圆心在定角∠α(0°<α<180°)的角平分线上运动,且⊙O与∠α的两边相切,图中阴影部分的面积S关于⊙O的半径r(r>0)变化的函数图象大致是
- A.

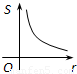
- B.

- C.

- D.

C
分析:连接OB、OC、OA,求出∠BOC的度数,求出AB、AC的长,求出四边形OBAC和扇形OBC的面积,即可求出答案.
解答: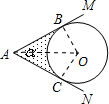 解:连接OB、OC、OA,
解:连接OB、OC、OA,
∵圆O切AM于B,切AN于C,
∴∠OBA=∠OCA=90°,OB=OC=r,AB=AC
∴∠BOC=360°-90°-90°-α=(180-α)°,
∵AO平分∠MAN,
∴∠BAO=∠CAO= α,
α,
AB=AC= ,
,
∴阴影部分的面积是:S四边形BACO-S扇形OBC=2× ×
× ×r-
×r-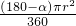 =(
=( -
- )r2,
)r2,
∵r>0,
∴S与r之间是二次函数关系.
故选C.
点评:本题主要考查对切线的性质,切线长定理,三角形和扇形的面积,锐角三角函数的定义,四边形的内角和定理等知识点的理解和掌握,能综合运用性质进行计算是解此题的关键.
分析:连接OB、OC、OA,求出∠BOC的度数,求出AB、AC的长,求出四边形OBAC和扇形OBC的面积,即可求出答案.
解答:
 解:连接OB、OC、OA,
解:连接OB、OC、OA,∵圆O切AM于B,切AN于C,
∴∠OBA=∠OCA=90°,OB=OC=r,AB=AC
∴∠BOC=360°-90°-90°-α=(180-α)°,
∵AO平分∠MAN,
∴∠BAO=∠CAO=
 α,
α,AB=AC=
 ,
,∴阴影部分的面积是:S四边形BACO-S扇形OBC=2×
 ×
× ×r-
×r-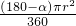 =(
=( -
- )r2,
)r2,∵r>0,
∴S与r之间是二次函数关系.
故选C.
点评:本题主要考查对切线的性质,切线长定理,三角形和扇形的面积,锐角三角函数的定义,四边形的内角和定理等知识点的理解和掌握,能综合运用性质进行计算是解此题的关键.

练习册系列答案
相关题目
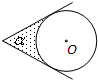 如图,⊙O的圆心在定角∠α(0°<α<180°)的角平分线上运动,且⊙O与∠α的两边相切,图中阴影部分的面积S关于⊙O的半径r(r>0)变化的函数图象大致是( )
如图,⊙O的圆心在定角∠α(0°<α<180°)的角平分线上运动,且⊙O与∠α的两边相切,图中阴影部分的面积S关于⊙O的半径r(r>0)变化的函数图象大致是( )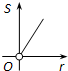
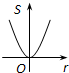
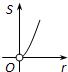
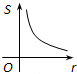
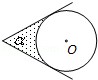
 B.
B. C.
C. D.
D.
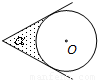 如图,⊙O的圆心在定角∠α(0°<α<180°)的角平分线上运动,且⊙O与∠α的两边相切,图中阴影部分的面积S关于⊙O的半径r(r>0)变化的函数图象大致是( )
如图,⊙O的圆心在定角∠α(0°<α<180°)的角平分线上运动,且⊙O与∠α的两边相切,图中阴影部分的面积S关于⊙O的半径r(r>0)变化的函数图象大致是( )
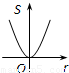
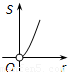
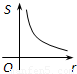
 如图,⊙O的圆心在定角∠α(0°<α<180°)的角平分线上运动,且⊙O与∠α的两边相切,图中阴影部分的面积S关于⊙O的半径r(r>0)变化的函数图象大致是( )
如图,⊙O的圆心在定角∠α(0°<α<180°)的角平分线上运动,且⊙O与∠α的两边相切,图中阴影部分的面积S关于⊙O的半径r(r>0)变化的函数图象大致是( )
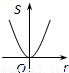
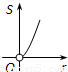

 如图,⊙O的圆心在定角∠α(0°<α<180°)的角平分线上运动,且⊙O与∠α的两边相切,图中阴影部分的面积S关于⊙O的半径r(r>0)变化的函数图象大致是( )
如图,⊙O的圆心在定角∠α(0°<α<180°)的角平分线上运动,且⊙O与∠α的两边相切,图中阴影部分的面积S关于⊙O的半径r(r>0)变化的函数图象大致是( )