题目内容
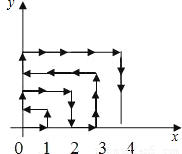
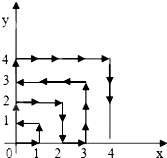如图，一个动点在第一象限内及x轴，y轴的正半轴上按一定的规则运动．在第一分钟时，它从原点运动到（1，0），第二分钟时从（1，0）运动到（1，1），而后它接着按图中箭头所示方向在与x轴，y轴平行的方向来回运动，且每分钟移动1个长度单位．在第57分钟结束时，这个动点所在位置的坐标是（6，7）
（6，7）
．分析：观察不难发现，点的个数按照平方数的规律变化，并且横坐标是奇数时按照运动方向点的纵坐标变大，横坐标是奇数时，按照运动方向点的纵坐标变小，求出与57最接近的平方数，然后解答即可．
解答：解：第57分钟结束时，点运动的路程是57，
∵72=49，57-49=8，
∴第57分钟结束时的点为从点（7，0）开始运动的第8个点，
坐标为（6，7）．
故答案为：（6，7）．
∵72=49，57-49=8，
∴第57分钟结束时的点为从点（7，0）开始运动的第8个点，
坐标为（6，7）．
故答案为：（6，7）．
点评：本题考查了点的坐标的变化规律，观察出点的个数按照平方数的规律变化是解题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
18、如图，一个动点在第一象限及x轴、y轴上运动，在第一秒钟，它从原点运动到（1，0），然后接着按图中箭头所示方向运动，即：（0，0）→（1，0）→（1，1）→（0，1）→…，且每秒移动一个单位，那么第2011秒时动点所在位置的坐标是
24、如图，一个动点在第一象限内及x轴，y轴上运动，在第一分钟，它从原点运动到（1，0），第二分钟，从（1，0）运动到（1，1），而后它接着按图中箭头所示在与x轴，y轴平行的方向来回运动，且每分钟运动1个单位长度．当动点所在位置分别是（5，5）时，所经过的时间是
