题目内容
2009年4月23日是我国海军成立60周年纪念日,为此我国邀请了20多个国家的代表团和部分海军舰艇来青岛港参加庆祝活动,出于安全考虑,我军在青岛海域设置了供各国舰艇停放的安全区域,规定在海岸线AB以外12海里范围内为安全区域,任何其他船只不得进入,并通过海岸线设立的相距30海里的A、B两处观测站来实施监控.某天发现一艘可疑船只行驶至C处,观测员甲在A处测得C位于A的北偏东30°方向,同时观测员乙在B处测得C位于B的北偏西45°方向.试通过计算说明观测员是否需要向可疑船只发出警告,令其退回?(规定 取1.4;
取1.4; 取1.7)
取1.7)
【答案】分析:根据题意即是比较C到AB的距离与12的大小,所以作CD⊥AB于D点,解三角形ABC求CD的长.
解答: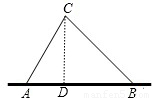 解:作CD⊥AB于D点,根据题意得:
解:作CD⊥AB于D点,根据题意得:
在Rt△ACD中,CD=AD•tan60°=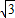 AD,即AD=
AD,即AD=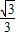 •CD.
•CD.
在Rt△BCD中,BD=CD•cot45°=CD×1=CD.
∵AB=AD+BD=30,
∴ CD+CD=30.
CD+CD=30.
解得CD=15(3- )≈19.5>12,
)≈19.5>12,
所以不需发出警告令其退回.
点评:化斜为直是解三角形的常规思路.本题因为涉及点到直线的距离,很自然想到作垂线构成直角三角形求解.
解答:
 解:作CD⊥AB于D点,根据题意得:
解:作CD⊥AB于D点,根据题意得:在Rt△ACD中,CD=AD•tan60°=
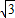 AD,即AD=
AD,即AD=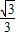 •CD.
•CD.在Rt△BCD中,BD=CD•cot45°=CD×1=CD.
∵AB=AD+BD=30,
∴
 CD+CD=30.
CD+CD=30.解得CD=15(3-
 )≈19.5>12,
)≈19.5>12,所以不需发出警告令其退回.
点评:化斜为直是解三角形的常规思路.本题因为涉及点到直线的距离,很自然想到作垂线构成直角三角形求解.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
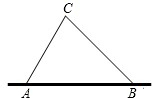 2009年4月23日是我国海军成立60周年纪念日,为此我国邀请了20多个国家的代表团和部分海军舰艇来青岛港参加庆祝活动,出于安全考虑,我军在青岛海域设置了供各国舰艇停放的安全区域,规定在海岸线AB以外12海里范围内为安全区域,任何其他船只不得进入,并通过海岸线设立的相距30海里的A、B两处观测站来实施监控.某天发现一艘可疑船只行驶至C处,观测员甲在A处测得C位于A的北偏东30°方向,同时观测员乙在B处测得C位于B的北偏西45°方向.试通过计算说明观测员是否需要向可疑船只发出警告,令其退回?(规定
2009年4月23日是我国海军成立60周年纪念日,为此我国邀请了20多个国家的代表团和部分海军舰艇来青岛港参加庆祝活动,出于安全考虑,我军在青岛海域设置了供各国舰艇停放的安全区域,规定在海岸线AB以外12海里范围内为安全区域,任何其他船只不得进入,并通过海岸线设立的相距30海里的A、B两处观测站来实施监控.某天发现一艘可疑船只行驶至C处,观测员甲在A处测得C位于A的北偏东30°方向,同时观测员乙在B处测得C位于B的北偏西45°方向.试通过计算说明观测员是否需要向可疑船只发出警告,令其退回?(规定 5个城市的国标标准时间(单位:时)在数轴上的表示(例如:伦敦时间的0点是汉城时间的9点)如图所示,为了庆祝中国人民解放军海军成立60周年,海上大阅兵在2009年4月23日14时20分在青岛附近黄海海域举行,请问北京时间2009年4月23日14时应是( )
5个城市的国标标准时间(单位:时)在数轴上的表示(例如:伦敦时间的0点是汉城时间的9点)如图所示,为了庆祝中国人民解放军海军成立60周年,海上大阅兵在2009年4月23日14时20分在青岛附近黄海海域举行,请问北京时间2009年4月23日14时应是( )