题目内容
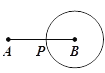
【题目】如图，已知A、B两个村庄的坐标分别为（2，3），（6，4），一辆汽车从原点O出发在x轴上行驶．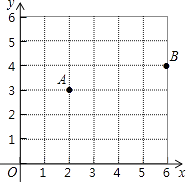
（1）汽车行驶到什么位置时离A村最近？写出此点的坐标；
（2）汽车行驶到什么位置时离B村最近？写出此点的坐标；
（3）汽车行驶到什么位置时，距离两村的和最短？请在图中画出这个位置，并求出此时汽车到两村距离的和．
【答案】
（1）解：由垂线段最短可知当汽车位于（2，0）处时，汽车距离A点最近
（2）解：由垂线段最短可知当汽车位于（6，0）处时，汽车距离B点最近
（3）解：如图所示：点C即为所求．
∵由轴对称的性质可知：AC=A′C，
∴AC+BC=A′C+BC=A′B= 
= 
【解析】（1）根据垂线段最短，可知汽车的位置及此点的坐标。
（2）根据垂线段最短，可知汽车的位置及此点的坐标。
（3）作点A关于x轴的对称点A
， 连接AB，交x轴于点C，点C为所求得的点，根据题意可知此时汽车到两村距离的和等于AB的长，再利用勾股定理求出AB的长即可。
【题目】某公司销售部有营销人员20人，销售部为了制定某种商品的月销售额，统计了这20人的销售额如下：
销售额（万元） | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
频数（个） | 1 | 1 | 5 | 4 | 3 | 2 | 3 | 1 |
（1）求这20位营销人员月销售额的平均数、中位数；
（2）假设你是销售部负责人，你认为把每位营销人员的月销售额定为多少合适？请说明你的理由．
【题目】甲、乙两人参加某网站的招聘测试，测试由网页制作和语言两个项目组成，他们各自的成绩（百分制）如下表所示：
应聘者 | 网页制作 | 语言 |
甲 | 80 | 70 |
乙 | 70 | 80 |
该网站根据成绩在两人之间录用了甲，则本次招聘测试中权重较大的是_____项目．
【题目】某酒店客房有三人间、双人间客房，收费数据如表所示：
普通（元／间／天） | 豪华（元／间／天） | |
三人间 | 150 | 300 |
双人间 | 140 | 400 |
为吸引游客，实行团体入住五折优惠措施，一个50人的旅游团优惠期间到该酒店入住，住了一些三人普通间和双人普通间客房，若每间客房正好住满，且一天共花去住宿费1510元，则旅游团住了三人普通间和双人普通间客房多少间？
