题目内容
（2002•广州）在半径为27m的圆形广场中央点O的上空安装了一个照明光源S，S′射向地面的光束呈圆锥形，其轴截面SAB的顶角为120°（如图）．求光源离地面的垂直高度SO（精确到0.1m，
=1.414，
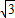=1.732，
=2.236，以上数据供参考）
【答案】分析：圆锥的高，底面上的半径，母线正好构成直角三角形，根据三角函数就可以求出．
解答：解：在△SAB中，SA=SB，
∵SO⊥AB
∴O是AB的中点．且∠ASO=∠BSO=60°．
在直角△ASO中，OA=27m．
∴tan60°=27÷SO
∴SO=27÷tan60°
∴SO=9
≈15.6m．
答：光源离地面的垂直高度SO为15.6m．
点评：本题考查了直角三角形的应用，三角函数的性质．属于常规题．
解答：解：在△SAB中，SA=SB，
∵SO⊥AB
∴O是AB的中点．且∠ASO=∠BSO=60°．
在直角△ASO中，OA=27m．
∴tan60°=27÷SO
∴SO=27÷tan60°
∴SO=9
≈15.6m．答：光源离地面的垂直高度SO为15.6m．
点评：本题考查了直角三角形的应用，三角函数的性质．属于常规题．
练习册系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
（2002•广州）在一次科技知识竞赛中，一组学生成绩统计如下：
这组学生成绩的中位数是 分．
| 分数 | 50 | 60 | 70 | 80 | 90 | 100 |
| 人数 | 2 | 5 | 10 | 13 | 14 | 6 |
（2002•广州）在一次科技知识竞赛中，一组学生成绩统计如下：
这组学生成绩的中位数是 分．
| 分数 | 50 | 60 | 70 | 80 | 90 | 100 |
| 人数 | 2 | 5 | 10 | 13 | 14 | 6 |