题目内容
(2005•哈尔滨)已知两个一次函数y1=-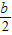 x-4和y2=
x-4和y2=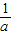 x+
x+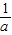 的图象重合,则一次函数y=ax+b的图象所经过的象限为( )
的图象重合,则一次函数y=ax+b的图象所经过的象限为( )A.第一、二、三象限
B.第二、三、四象限
C.第一、三、四象限
D.第一、二、四象限
【答案】分析:首先根据两个一次函数y1=- x-4和y2=
x-4和y2=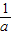 x+
x+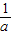 的图象重合,求出a、b的值,然后根据a、b的值确定一次函数y=ax+b的图象所经过的象限.
的图象重合,求出a、b的值,然后根据a、b的值确定一次函数y=ax+b的图象所经过的象限.
解答:解:两个一次函数y1=-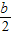 x-4和y2=
x-4和y2= x+
x+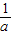 的图象重合,
的图象重合,
则-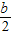 =
=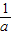 ,-4=
,-4= ,
,
解得a=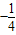 ,b=8.
,b=8.
一次函数y=ax+b的一次项系数a<0,则y随x的增大而减小,函数经过二,四象限;
常数项b>0,则函数与y轴正半轴相交,因而函数经过一、二象限.
则一次函数y=ax+b的图象所经过的象限为第一、二、四象限.
故选D.
点评:两直线y=kx+b所在的位置与k、b的关系:k1=k2,b1=b2?两直线重合;k1=k2,b1≠b2?两直线平行;k1≠k2?两直线相交.函数值y随x的增大而减小?k<0;函数值y随x的增大而增大?k>0;一次函数y=kx+b图象与y轴的正半轴相交?b>0,一次函数y=kx+b图象与y轴的负半轴相交?b<0,一次函数y=kx+b图象过原点?b=0.
 x-4和y2=
x-4和y2=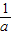 x+
x+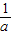 的图象重合,求出a、b的值,然后根据a、b的值确定一次函数y=ax+b的图象所经过的象限.
的图象重合,求出a、b的值,然后根据a、b的值确定一次函数y=ax+b的图象所经过的象限.解答:解:两个一次函数y1=-
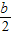 x-4和y2=
x-4和y2= x+
x+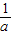 的图象重合,
的图象重合,则-
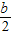 =
=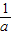 ,-4=
,-4= ,
,解得a=
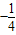 ,b=8.
,b=8.一次函数y=ax+b的一次项系数a<0,则y随x的增大而减小,函数经过二,四象限;
常数项b>0,则函数与y轴正半轴相交,因而函数经过一、二象限.
则一次函数y=ax+b的图象所经过的象限为第一、二、四象限.
故选D.
点评:两直线y=kx+b所在的位置与k、b的关系:k1=k2,b1=b2?两直线重合;k1=k2,b1≠b2?两直线平行;k1≠k2?两直线相交.函数值y随x的增大而减小?k<0;函数值y随x的增大而增大?k>0;一次函数y=kx+b图象与y轴的正半轴相交?b>0,一次函数y=kx+b图象与y轴的负半轴相交?b<0,一次函数y=kx+b图象过原点?b=0.

练习册系列答案
相关题目
 x+a与(1)中所求的抛物线交于M、N两点,问:是否存在a的值,使得∠MON=90°?若存在,求出a的值;若不存在,请说明理由.
x+a与(1)中所求的抛物线交于M、N两点,问:是否存在a的值,使得∠MON=90°?若存在,求出a的值;若不存在,请说明理由.

 x+a与(1)中所求的抛物线交于M、N两点,问:是否存在a的值,使得∠MON=90°?若存在,求出a的值;若不存在,请说明理由.
x+a与(1)中所求的抛物线交于M、N两点,问:是否存在a的值,使得∠MON=90°?若存在,求出a的值;若不存在,请说明理由.
 x+a与(1)中所求的抛物线交于M、N两点,问:是否存在a的值,使得∠MON=90°?若存在,求出a的值;若不存在,请说明理由.
x+a与(1)中所求的抛物线交于M、N两点,问:是否存在a的值,使得∠MON=90°?若存在,求出a的值;若不存在,请说明理由.