题目内容
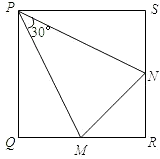如图，在正方形PQRS中，M、N分别为QR、RS上的点，且∠MPN=30°．若△PMN为等腰三角形，且面积为1，则正方形PQRS的面积为________．
3
分析：根据三角形面积计算公式即可求得PM的长度，根据PM的长度和∠MPQ即可求得PQ的长度，根据正方形面积计算公式即可解题．
解答：S△PMN=
×PM×PM×sin30°，
∴PM×PM=4，PM=2，
∵∠MPQ=∠NPS，
∴∠MPQ=∠NPS=30°．
∴PQ=PMcos30°=
，
∴正方形面积为PQ2=3．
故答案为 3．
点评：本题考查了三角形面积的计算公式，考查了特殊角的三角函数值，考查了直角三角形中三角函数的应用，考查了正方形面积的计算，本题中求PQ的长是解题的关键．
分析：根据三角形面积计算公式即可求得PM的长度，根据PM的长度和∠MPQ即可求得PQ的长度，根据正方形面积计算公式即可解题．
解答：S△PMN=
×PM×PM×sin30°，∴PM×PM=4，PM=2，
∵∠MPQ=∠NPS，
∴∠MPQ=∠NPS=30°．
∴PQ=PMcos30°=
，∴正方形面积为PQ2=3．
故答案为 3．
点评：本题考查了三角形面积的计算公式，考查了特殊角的三角函数值，考查了直角三角形中三角函数的应用，考查了正方形面积的计算，本题中求PQ的长是解题的关键．
练习册系列答案
相关题目
29、如图：在正方形ABCD中，点P、Q是CD边上的两点，且DP=CQ，过D作DG⊥AP于H，交AC、BC分别于E，G，AP、EQ的延长线相交于R．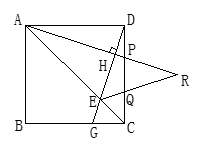
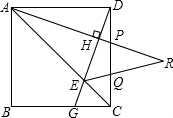、EQ的延长线相交于R．