题目内容
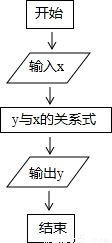
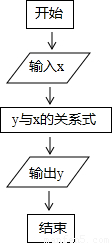
按如图所示的流程,输入一个数据x,根据y与x的关系式就输出一个数据y,这样可以将一组数据变换成另一组新的数据,要使任意一组都在20~100(含20和100)之间的数据,变换成一组新数据后能满足下列两个要求:(Ⅰ)新数据都在60~100(含60和100)之间;
(Ⅱ)新数据之间的大小关系与原数据之间的大小关系一致,即原数据大的对应的新数据也较大.
(1)若y与x的关系是y=x+p(100-x),请说明:当p=
 时,这种变换满足上述两个要求;
时,这种变换满足上述两个要求;(2)若按关系式y=a(x-h)2+k(a>0)将数据进行变换,请写出一个满足上述要求的这种关系式.(不要求对关系式符合题意作说明,但要写出关系式得出的主要过程)
【答案】分析:(1)当P= 时,y=
时,y= x+50,观察这个一次函数可知:斜率>0,则y随x的增大而增大,因此符合条件Ⅱ;因为20≤x≤100,即20≤2y-100≤100,可得60≤y≤100,因此也符合Ⅰ的条件.
x+50,观察这个一次函数可知:斜率>0,则y随x的增大而增大,因此符合条件Ⅱ;因为20≤x≤100,即20≤2y-100≤100,可得60≤y≤100,因此也符合Ⅰ的条件.
(2)本题答案不唯一.可根据抛物线的开口方向和抛物线的对称轴来说明.
解答:解:(1)当P= 时,y=x+
时,y=x+ (100-x),
(100-x),
即y= x+50.
x+50.
∴y随着x的增大而增大,
即P= 时,满足条件(Ⅱ)
时,满足条件(Ⅱ)
又当x=20时,y= ×20+50=60.
×20+50=60.
而原数据都在20~100之间,
所以新数据都在60~100之间,即满足条件(Ⅰ),
综上可知,当P= 时,这种变换满足要求.
时,这种变换满足要求.
(2)本题是开放性问题,答案不唯一.
若所给出的关系式满足:
(a)h≤20;
(b)若x=20,100时,y的对应值m,n能落在60~100之间,则这样的关系式都符合要求.
如取h=20,y=a(x-20)2+k,
∵a>0,
∴当20≤x≤100时,y随着x的增大而增大,
令x=20,y=60,得k=60 ①
令x=100,y=100,得a×802+k=100②
由①②解得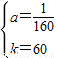 ,
,
∴y=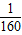 (x-20)2+60.
(x-20)2+60.
点评:本题考查了一次函数和二次函数的性质,解题的关键是弄清题目给出的阅读材料的含义.
 时,y=
时,y= x+50,观察这个一次函数可知:斜率>0,则y随x的增大而增大,因此符合条件Ⅱ;因为20≤x≤100,即20≤2y-100≤100,可得60≤y≤100,因此也符合Ⅰ的条件.
x+50,观察这个一次函数可知:斜率>0,则y随x的增大而增大,因此符合条件Ⅱ;因为20≤x≤100,即20≤2y-100≤100,可得60≤y≤100,因此也符合Ⅰ的条件.(2)本题答案不唯一.可根据抛物线的开口方向和抛物线的对称轴来说明.
解答:解:(1)当P=
 时,y=x+
时,y=x+ (100-x),
(100-x),即y=
 x+50.
x+50.∴y随着x的增大而增大,
即P=
 时,满足条件(Ⅱ)
时,满足条件(Ⅱ)又当x=20时,y=
 ×20+50=60.
×20+50=60.而原数据都在20~100之间,
所以新数据都在60~100之间,即满足条件(Ⅰ),
综上可知,当P=
 时,这种变换满足要求.
时,这种变换满足要求.(2)本题是开放性问题,答案不唯一.
若所给出的关系式满足:
(a)h≤20;
(b)若x=20,100时,y的对应值m,n能落在60~100之间,则这样的关系式都符合要求.
如取h=20,y=a(x-20)2+k,
∵a>0,
∴当20≤x≤100时,y随着x的增大而增大,
令x=20,y=60,得k=60 ①
令x=100,y=100,得a×802+k=100②
由①②解得
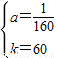 ,
,∴y=
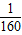 (x-20)2+60.
(x-20)2+60.点评:本题考查了一次函数和二次函数的性质,解题的关键是弄清题目给出的阅读材料的含义.

练习册系列答案
相关题目
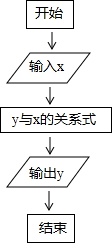 按如图所示的流程,输入一个数据x,根据y与x的关系式就输出一个数据y,这样可以将一组数据变换成另一组新的数据,要使任意一组都在20~100(含20和100)之间的数据,变换成一组新数据后能满足下列两个要求:
按如图所示的流程,输入一个数据x,根据y与x的关系式就输出一个数据y,这样可以将一组数据变换成另一组新的数据,要使任意一组都在20~100(含20和100)之间的数据,变换成一组新数据后能满足下列两个要求: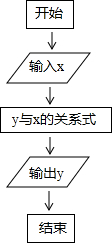 按如图所示的流程,输入一个数据x,根据y与x的关系式就输出一个数据y,这样可以将一组数据变换成另一组新的数据,要使任意一组都在20~100(含20和100)之间的数据,变换成一组新数据后能满足下列两个要求:
按如图所示的流程,输入一个数据x,根据y与x的关系式就输出一个数据y,这样可以将一组数据变换成另一组新的数据,要使任意一组都在20~100(含20和100)之间的数据,变换成一组新数据后能满足下列两个要求: 时,这种变换满足上述两个要求;
时,这种变换满足上述两个要求; 时,这种变换满足上述两个要求;
时,这种变换满足上述两个要求;