题目内容
如下图，AD是∠BAC的平分线，DE垂直AB于点E，DF垂直AC于点F，且BD=DC．求证：BE=CF．
证明：∵DE⊥AB，DF⊥AC，
∴∠E=∠DFC=90°．
∵AD平分∠EAC，
∴DE=DF．
在Rt△DBE和Rt△DCF中，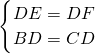
∴Rt△DBE≌Rt△CDF（HL）．
∴BE=CF．
分析：根据角平分线的性质可得到DE=DF，由已知可得∠E=∠DFC=90°，从而可利用HL来判定Rt△DBE≌Rt△CDF，由全等三角形的性质即可得到BE=CF．
点评：本题考查了三角形全等的判定及性质；做题时利用了角平分线的性质，得到线段相等，这也是解决本题的关键．
∴∠E=∠DFC=90°．
∵AD平分∠EAC，
∴DE=DF．
在Rt△DBE和Rt△DCF中，
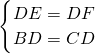
∴Rt△DBE≌Rt△CDF（HL）．
∴BE=CF．
分析：根据角平分线的性质可得到DE=DF，由已知可得∠E=∠DFC=90°，从而可利用HL来判定Rt△DBE≌Rt△CDF，由全等三角形的性质即可得到BE=CF．
点评：本题考查了三角形全等的判定及性质；做题时利用了角平分线的性质，得到线段相等，这也是解决本题的关键．
练习册系列答案
相关题目
，BC=
。
，求△COD的面积；
