题目内容

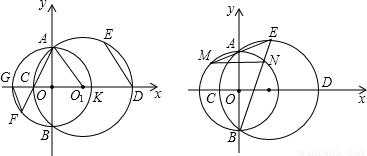
已知：如图1，点O₁在x轴的正半轴上，⊙O₁与x轴交于C、D两点，半径为4的⊙O与x轴的负半轴交于G点．⊙O与⊙O₁的交点A、B在y轴上，设⊙O₁的弦AC的延长线交⊙O于F点，连接GF，且AF=2

2

GF
（1）求证：C为线段OG的中点；
（2）连接AO₁，作⊙O₁的弦DE，使DE∥AO₁，求E点的坐标；
（3）如图2，线段EA、EB（或它们的延长线）分别交⊙O于点M、N．

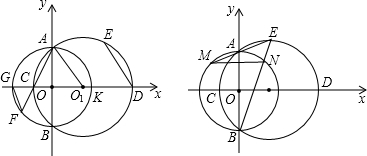
问：当点E在（不含端点A、B）上运动时，线段MN的长度是否会发生变化？试证明你的结论．

分析：（1）证明：连接AG，易得△AGC∽△AFG，又AF=2

2

GF，可得⊙O的半径为4，则AG=4

2

，
GC=2=

1

2

OG，即可得结论；
（2）连接OE交AO₁于点H，作EK⊥CD于K，易得Rt△AOO₁≌Rt△CHO₁，又由O₁H∥DE，且CO₁=O₁D，可得ED=2HO₁=6，有三角函数的定义可得EK与OKD的值，进而可得点E的坐标；
（3）当点E在上运动时，MN的长度不变；易得△EMN∽△EBA，进而连接AN，则AN⊥BE，∠ANE=90°，

EN

AE

=cos∠E，MN=AB•cos∠E=8cos∠E，分析可得结论．

解答：

（1）证明：连接AG，
∵OA⊥OG，OA=OG，
∴∠AGC=∠AFG=45°，∠GAC=∠FAG，
∴△AGC∽△AFG，
又AF=2

2

GF，
∴

AG

GC

=

AF

FG

=2

2

，
∵⊙O的半径为4，
∴AG=4

2

，
∴GC=2=

1

2

OG，
即点C为线段OG的中点；

（2）解：连接OE交AO₁于点H，作EK⊥CD于K，
∵AO₁∥ED，DE⊥CE，
∴O₁A⊥CE，
∵OA=4，OC=

1

2

OG=2，OA²=OC×OD，
∴OD=8，O₁O=3，
∴Rt△AOO₁≌Rt△CHO₁，
∴O₁H=O₁O=3，
又∵O₁H∥DE，CO₁=O₁D，
∴ED=2HO₁=6，
∴sin∠EDK=sin∠AO₁O=

4

5

，cos∠EDK=

3

5

，
在Rt△EDK中，EK=ED×sin∠EDK=6×

4

5

=

24

5

，
KD=ED×cos∠EDK=6×

3

5

=

18

5

，
OK=OD-KD=

22

5

，
故，点E的坐标为（

22

5

，

24

5

）；

（3）解：当点E在上运动时，MN的长度不变；
在△EMN和△EBA中，∵∠E=∠E，∠EMN=∠EBA，
∴△EMN∽△EBA．
∴

MN

BA

=

EN

EA

，
即MN=

EN

EA

×AB，
连接AN，则AN⊥BE，∠ANE=90°，

EN

AE

=cos∠E，MN=AB×cos∠E=8cos∠E，
当点E在上运动时，∠E的大小不变，8cos∠E是常量，故MN的长度不变．

点评：本题主要考查弦切角定理，相似三角形的判定及平行线的性质，难度较大．

练习册系列答案

西城学科专项测试系列答案

小考必做系列答案

小考实战系列答案

小考复习精要系列答案

小考总动员系列答案

小升初必备冲刺48天系列答案

68所名校图书小升初高分夺冠真卷系列答案

伴你成长周周练月月测系列答案

小升初金卷导练系列答案

萌齐小升初强化模拟训练系列答案

相关题目

已知：如图1，点O₁在x轴的正半轴上，⊙O₁与x轴交于C、D两点，半径为4的⊙O与x轴的负半轴交于G点．⊙O与⊙O₁的交点A、B在y轴上，设⊙O₁的弦AC的延长线交⊙O于F点，连接GF，且AF=2 $数学公式$ GF
（1）求证：C为线段OG的中点；
（2）连接AO₁，作⊙O₁的弦DE，使DE∥AO₁，求E点的坐标；
（3）如图2，线段EA、EB（或它们的延长线）分别交⊙O于点M、N．问：当点E在（不含端点A、B）上运动时，线段MN的长度是否会发生变化？试证明你的结论．

（2000•武汉）已知：如图1，点O₁在x轴的正半轴上，⊙O₁与x轴交于C、D两点，半径为4的⊙O与x轴的负半轴交于G点．⊙O与⊙O₁的交点A、B在y轴上，设⊙O₁的弦AC的延长线交⊙O于F点，连接GF，且AF=2

GF
（1）求证：C为线段OG的中点；
（2）连接AO₁，作⊙O₁的弦DE，使DE∥AO₁，求E点的坐标；
（3）如图2，线段EA、EB（或它们的延长线）分别交⊙O于点M、N．问：当点E在（不含端点A、B）上运动时，线段MN的长度是否会发生变化？试证明你的结论．

（2000•武汉）已知：如图1，点O₁在x轴的正半轴上，⊙O₁与x轴交于C、D两点，半径为4的⊙O与x轴的负半轴交于G点．⊙O与⊙O₁的交点A、B在y轴上，设⊙O₁的弦AC的延长线交⊙O于F点，连接GF，且AF=2

GF
（1）求证：C为线段OG的中点；
（2）连接AO₁，作⊙O₁的弦DE，使DE∥AO₁，求E点的坐标；
（3）如图2，线段EA、EB（或它们的延长线）分别交⊙O于点M、N．问：当点E在（不含端点A、B）上运动时，线段MN的长度是否会发生变化？试证明你的结论．

（2000•武汉）已知：如图1，点O₁在x轴的正半轴上，⊙O₁与x轴交于C、D两点，半径为4的⊙O与x轴的负半轴交于G点．⊙O与⊙O₁的交点A、B在y轴上，设⊙O₁的弦AC的延长线交⊙O于F点，连接GF，且AF=2

GF
（1）求证：C为线段OG的中点；
（2）连接AO₁，作⊙O₁的弦DE，使DE∥AO₁，求E点的坐标；
（3）如图2，线段EA、EB（或它们的延长线）分别交⊙O于点M、N．问：当点E在（不含端点A、B）上运动时，线段MN的长度是否会发生变化？试证明你的结论．