题目内容
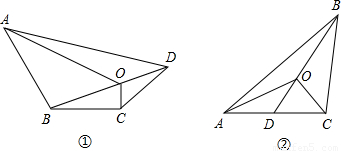
四边形是大家最熟悉的图形之一,我们已经发现了它的许多性质.只要善于观察、乐于探索,我们还会发现更多的结论.(1)四边形一条对角线上任意一点与另外两个顶点的连线,将四边形分成四个三角形(如图①),其中相对的两对三角形的面积之积相等.你能证明这个结论吗?试试看.
已知:在四边形ABCD中,O是对角线BD上任意一点.(如图①)
求证:S△OBC•S△OAD=S△OAB•S△OCD;
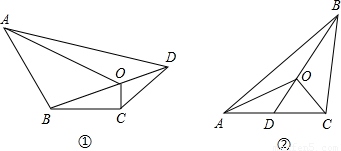
(2)在三角形中(如图②),你能否归纳出类似的结论?若能,写出你猜想的结论,并证明:若不能,说明理由.
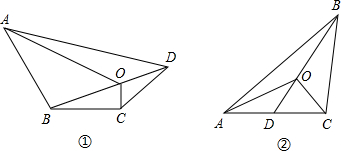
分析:(1)根据三角形的面积公式,则应分别分别过点A、C,做AE⊥DB,交DB的延长线于E,CF⊥BD于F.然后根据三角形的面积公式分别计算要证明的等式的左边和右边即可;
(2)根据(1)中的思路,显然可以归纳出:从三角形的一个顶点与对边上任意一点的连线上任取一点,与三角形的另外两个顶点连线,将三角形分成四个小三角形,其中相对的两对三角形的面积之积相等.证明思路类似.
(2)根据(1)中的思路,显然可以归纳出:从三角形的一个顶点与对边上任意一点的连线上任取一点,与三角形的另外两个顶点连线,将三角形分成四个小三角形,其中相对的两对三角形的面积之积相等.证明思路类似.
解答: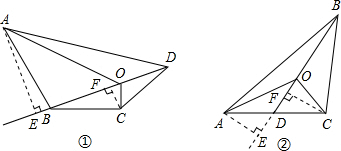
证明:(1)分别过点A、C,做AE⊥DB,交DB的延长线于E,CF⊥BD于F,
则有:S△AOB=
BO•AE,
S△COD=
DO•CF,
S△AOD=
DO•AE,
S△BOC=
BO•CF,
∴S△AOB•S△COD=
BO•DO•AE•CF,
S△AOD•S△BOC=
BO•DO•CF•AE,
∴S△AOB•S△COD=S△AOD•S△BOC.(4分);
(2)能.
从三角形的一个顶点与对边上任意一点的连线上任取一点,与三角形的另外两个顶点连线,将三角形分成四个小三角形,其中相对的两对三角形的面积之积相等.
或S△AOD•S△BOC=S△AOB•S△DOC,(5分)
已知:在△ABC中,D为AC上一点,O为BD上一点,
求证:S△AOD•S△BOC=S△AOB•S△DOC.
证明:分别过点A、C,作AE⊥BD,交BD的延长线于E,作CF⊥BD于F,
则有:S△AOD=
DO•AE,S△BOC=
BO•CF,
S△OAB=
OB•AE,S△DOC=
OD•CF,
∴S△AOD•S△BOC=
OB•OD•AE•CF,
S△OAB•S△DOC=
BO•OD•AE•CF,
∴S△AOD•S△BOC=S△OAB•S△DOC.

证明:(1)分别过点A、C,做AE⊥DB,交DB的延长线于E,CF⊥BD于F,
则有:S△AOB=
| 1 |
| 2 |
S△COD=
| 1 |
| 2 |
S△AOD=
| 1 |
| 2 |
S△BOC=
| 1 |
| 2 |
∴S△AOB•S△COD=
| 1 |
| 4 |
S△AOD•S△BOC=
| 1 |
| 4 |
∴S△AOB•S△COD=S△AOD•S△BOC.(4分);
(2)能.
从三角形的一个顶点与对边上任意一点的连线上任取一点,与三角形的另外两个顶点连线,将三角形分成四个小三角形,其中相对的两对三角形的面积之积相等.
或S△AOD•S△BOC=S△AOB•S△DOC,(5分)
已知:在△ABC中,D为AC上一点,O为BD上一点,
求证:S△AOD•S△BOC=S△AOB•S△DOC.
证明:分别过点A、C,作AE⊥BD,交BD的延长线于E,作CF⊥BD于F,
则有:S△AOD=
| 1 |
| 2 |
| 1 |
| 2 |
S△OAB=
| 1 |
| 2 |
| 1 |
| 2 |
∴S△AOD•S△BOC=
| 1 |
| 4 |
S△OAB•S△DOC=
| 1 |
| 4 |
∴S△AOD•S△BOC=S△OAB•S△DOC.
点评:恰当地作出三角形的高,根据三角形的面积公式进行证明.

练习册系列答案
 每课必练系列答案
每课必练系列答案
相关题目