题目内容
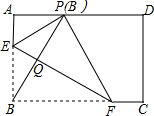 如图,在矩形ABCD中,点E,F分别在边AB,BC上,且AE=
如图,在矩形ABCD中,点E,F分别在边AB,BC上,且AE=| 1 |
| 3 |
| A、①② | B、②③ | C、①③ | D、①④ |
练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
下列图形是轴对称图形的是( )
A、 | B、 | C、 | D、 |
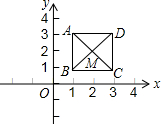 如图,已知正方形ABCD,顶点A(1,3)、B(1,1)、C(3,1).规定“把正方形ABCD先沿x轴翻折,再向左平移1个单位”为一次变换,如此这样,连续经过2014次变换后,正方形ABCD的对角线交点M的坐标变为( )
如图,已知正方形ABCD,顶点A(1,3)、B(1,1)、C(3,1).规定“把正方形ABCD先沿x轴翻折,再向左平移1个单位”为一次变换,如此这样,连续经过2014次变换后,正方形ABCD的对角线交点M的坐标变为( )| A、(-2012,2) | B、(-2012,-2) | C、(-2013,-2) | D、(-2013,2) |
用矩形纸片折出直角的平分线,下列折法正确的是( )
A、 | B、 | C、 | D、 |
已知ABCD是一张四边行纸片,其中AB<BC,将四边形沿BD所在的直线折叠,点A恰好落在BC上(如图①),展开后出现折现BD(如图②);再将点B折向点D,是B、D两点重迭(如图③),展开后出现折现CE(如图④).则下列结论正确的是( )
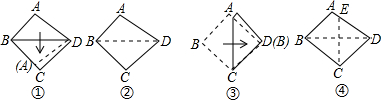

| A、∠ADB=∠BDC | B、∠ADB>∠BDC | C、AD∥BC | D、AB∥CD |
 将矩形纸片ABCD按如图所示的方式折叠,AE、EF为折痕,折叠后,点C落在AD边上的C1处,并且点B落在EC1边上的B1处.若∠BAE=30°,AB=
将矩形纸片ABCD按如图所示的方式折叠,AE、EF为折痕,折叠后,点C落在AD边上的C1处,并且点B落在EC1边上的B1处.若∠BAE=30°,AB=| 3 |
A、
| ||
| B、2 | ||
| C、3 | ||
D、2
|
如图,将正方形ABCD的四个角向内折起,恰好拼成一个无缝隙无重叠的四边形EFGH,再将四边形EFGH的一个角向内折起,使点F恰好和EG的中点重合,折为IJ,若点H到IJ的距离HK=12cm,则边AB的长是( )
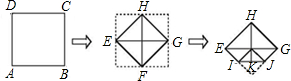

| A、16cm | B、12cm | C、9cm | D、8cm |
 甲、乙两人在一次百米赛跑中,路程s(米)与赛跑时间t(秒)的关系如图,则下列说法正确的是( )
甲、乙两人在一次百米赛跑中,路程s(米)与赛跑时间t(秒)的关系如图,则下列说法正确的是( )| A、乙先到达终点 | B、乙比甲跑的路程多 | C、乙用的时间短 | D、甲的速度比乙的速度快 |

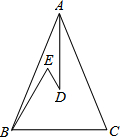 如图,在△ABC中,AB=AC,D、E是△ABC内两点,AD平分∠BAC,∠EBC=∠E=60°,若BE=60cm,DE=2cm,则BC=
如图,在△ABC中,AB=AC,D、E是△ABC内两点,AD平分∠BAC,∠EBC=∠E=60°,若BE=60cm,DE=2cm,则BC=