题目内容
 如图,矩形草坪ABCD中,AD=10m,AB=10
如图,矩形草坪ABCD中,AD=10m,AB=10| 3 |
| A、9.5m2 |
| B、10.0m2 |
| C、10.5m2 |
| D、11.0m2 |
分析:由四边形ABCD为矩形得到△ADB为直角三角形,又∵AD=10,AB=10
,由此利用勾股定理求出BD=20,又∵cos∠ADB=
=
,∴∠ADB=60°,又矩形对角线互相平分且相等,便道的宽为1m,所以每个扇环都是圆心角为30°且外环半径为10.5,内环半径为9.5.这样可以求出每个扇环的面积.
| 3 |
| AD |
| DB |
| 1 |
| 2 |
解答: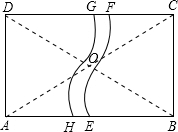 解:∵四边形ABCD为矩形,
解:∵四边形ABCD为矩形,
∴△ADB为直角三角形,
又∵AD=10,AB=10
,
∴BD=
=20,
又∵cos∠ADB=
=
,
∴∠ADB=60°.
又矩形对角线互相平分且相等,便道的宽为1m,
所以每个扇环都是圆心角为30°,且外环半径为10.5,内环半径为9.5.
∴每个扇环的面积为
-
=
.
∴当π取3.14时整条便道面积为
×2=10.4666≈10.5m2.
便道面积约为10.5m2.
故选C.
 解:∵四边形ABCD为矩形,
解:∵四边形ABCD为矩形,∴△ADB为直角三角形,
又∵AD=10,AB=10
| 3 |
∴BD=
| AD2+AB2 |
又∵cos∠ADB=
| AD |
| BD |
| 1 |
| 2 |
∴∠ADB=60°.
又矩形对角线互相平分且相等,便道的宽为1m,
所以每个扇环都是圆心角为30°,且外环半径为10.5,内环半径为9.5.
∴每个扇环的面积为
| 30×10.52π |
| 360 |
| 30×9.52π |
| 360 |
| 5π |
| 3 |
∴当π取3.14时整条便道面积为
| 5π |
| 3 |
便道面积约为10.5m2.
故选C.
点评:此题考查内容比较多,有勾股定理、三角函数、扇形面积,做题的关键是把实际问题转化为数学问题.

练习册系列答案
相关题目
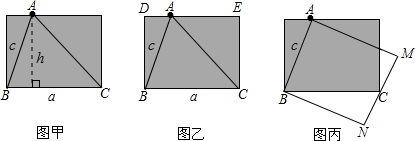
 ah=100可得ah=200,∵c>h,∴ac>200.
ah=100可得ah=200,∵c>h,∴ac>200.