题目内容
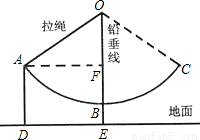
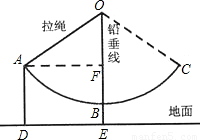
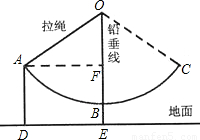
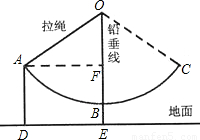
 如图,秋千拉绳OB的长为3米,静止时,踏板到地面的距离BE长时0.6米(踏板的厚度忽略不计),小亮荡该秋千时,当秋千拉绳有OB运动到OA时,拉绳OA与铅垂线OE的夹角为55°,请你计算此时该秋千踏板离地面的高度AD是多少米?(精确到0.1米)
如图,秋千拉绳OB的长为3米,静止时,踏板到地面的距离BE长时0.6米(踏板的厚度忽略不计),小亮荡该秋千时,当秋千拉绳有OB运动到OA时,拉绳OA与铅垂线OE的夹角为55°,请你计算此时该秋千踏板离地面的高度AD是多少米?(精确到0.1米)
解:如图,在Rt△AFO中,∠AFO=90°,
∴cos∠AOF=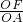 ,
,
∴OF=OA•cos∠AOF,
又∵OA=OB=3,∠AOF=55°,
∴OF=3•cos55°≈1.72,
∴EF=3+0.6-1.72≈1.9,
∴AD=EF≈1.9.
分析:由题可知,AD=EF,所以,要求出AD或EF,必须要有OF的长,在直角三角形OAF中,∠AOF=55°,OA=3,有OF=OA•cos∠AOF=3cos55°≈1.72,∴EF=3+0.6-1.72≈1.9,即AD=EF=1.9.
点评:解此题关键是把实际问题转化为数学问题,把实际问题抽象到三角形中,利用三角函数解答.
∴cos∠AOF=
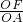 ,
,∴OF=OA•cos∠AOF,
又∵OA=OB=3,∠AOF=55°,
∴OF=3•cos55°≈1.72,
∴EF=3+0.6-1.72≈1.9,
∴AD=EF≈1.9.
分析:由题可知,AD=EF,所以,要求出AD或EF,必须要有OF的长,在直角三角形OAF中,∠AOF=55°,OA=3,有OF=OA•cos∠AOF=3cos55°≈1.72,∴EF=3+0.6-1.72≈1.9,即AD=EF=1.9.
点评:解此题关键是把实际问题转化为数学问题,把实际问题抽象到三角形中,利用三角函数解答.

练习册系列答案
相关题目
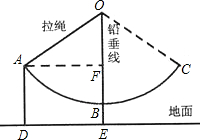 如图,秋千拉绳OB的长为3米,静止时,踏板到地面的距离BE长时0.6米(踏板的厚度忽略不计),小亮荡该秋千时,当秋千拉绳有OB运动到OA时,拉绳OA与铅垂线OE的夹角为55°,请你计算此时该秋千踏板离地面的高度AD是多少米?(精确到0.1米)
如图,秋千拉绳OB的长为3米,静止时,踏板到地面的距离BE长时0.6米(踏板的厚度忽略不计),小亮荡该秋千时,当秋千拉绳有OB运动到OA时,拉绳OA与铅垂线OE的夹角为55°,请你计算此时该秋千踏板离地面的高度AD是多少米?(精确到0.1米)