题目内容
如图直线l1//l2,AB⊥CD,∠1=34°,那么∠2的度数是 

56°
根据垂直的定义得到∠4=90°,根据三角形外角性质有∠4=∠1+∠3,则∠3=90°-∠1=90°-34°=56°,由l1∥l2,根据两直线平行,同位角相等即可得到
∠2=∠3=56°.
解:如图,
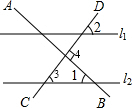
∵AB⊥CD,
∴∠4=90°,
又∵∠4=∠1+∠3,
∴∠3=90°-∠1=90°-34°=56°,
∵l1∥l2,
∴∠2=∠3=56°.
故答案为56.
∠2=∠3=56°.
解:如图,

∵AB⊥CD,
∴∠4=90°,
又∵∠4=∠1+∠3,
∴∠3=90°-∠1=90°-34°=56°,
∵l1∥l2,
∴∠2=∠3=56°.
故答案为56.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

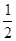 BC,
BC, 
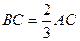 ,D为BC的中点,求BC、AD的长
,D为BC的中点,求BC、AD的长