题目内容
【题目】如图所示,△ABC平移后得到△DEF.
(1)若∠A=80°,∠E=60°,求∠C的度数;
(2)若AC=BC,BC与DF相交于点O,则OD与OB相等吗?说明理由.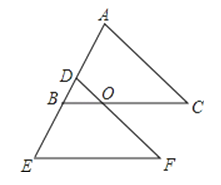
【答案】解:(1)∵△ABC平移后得到△DEF,
∴∠ABC=∠E=60°,
在△ABC中,∠C=180°﹣∠A﹣∠ABC=180°﹣80°﹣60°=40°;
(2)OD=OB.
理由如下:∵AC=BC,
∴∠A=∠ABC,
由平移的性质得,∠A=∠EDF,
∴∠ABC=∠EDF,
∴OD=OB.
【解析】(1)根据平移变换只改变图形的位置不改变图形的形状可得∠ABC=∠E,再根据三角形的内角和等于180°列式计算即可得解;
(2)根据等边对等角可得∠A=∠ABC,再根据平移的性质求出∠A=∠EDF,然后求出∠ABC=∠EDF,最后利用等角对等边解答即可.
【考点精析】关于本题考查的平移的性质,需要了解①经过平移之后的图形与原来的图形的对应线段平行(或在同一直线上)且相等,对应角相等,图形的形状与大小都没有发生变化;②经过平移后,对应点所连的线段平行(或在同一直线上)且相等才能得出正确答案.

练习册系列答案
相关题目

