题目内容
 如图下列条件
如图下列条件
①AC⊥BD、OC=OA;②∠1=∠2=∠3=∠4;③OA=OC、OB=OD、AC⊥BD;④AB=BC=CD、AC⊥BD.
一定能判定四边形ABCD为菱形的有
- A.1个
- B.2个
- C.3个
- D.4个
C
分析:根据菱形的判定方法有三种:①定义:一组邻边相等的平行四边形是菱形;②四边相等的四边形是菱形;③对角线互相垂直平分的四边形是菱形分别判定即可,
解答: 证明:①当AC⊥BD、OC=OA,不能确定BO是否等于DO,故不能判定四边形ABCD为菱形,故此选项错误;
证明:①当AC⊥BD、OC=OA,不能确定BO是否等于DO,故不能判定四边形ABCD为菱形,故此选项错误;
②∵∠1=∠2=∠3=∠4
∴AB=AD,BC=CD,
在△ABD和△CBD中,
∵ ,
,
∴△ABD≌△CBD,
∴AB=BC,AD=CD,
∴AB=BC=AD=CD;
故四边形ABCD为菱形,故此选项正确;
③∵OA=OC、OB=OD,
∴四边形ABCD为平行四边形,
又∵AC⊥BD,
∴平行四边形ABCD为菱形,故此选项正确;
 ④∵AB=BC=CD,AC⊥BD,
④∵AB=BC=CD,AC⊥BD,
∴在Rt△BOC和Rt△DOC中,
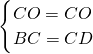
∴Rt△BOC≌Rt△DOC(HL),
∴BO=DO,
∴在Rt△ABO和Rt△ADO中,

∴△ABO≌△ADO(SAS),
∴AB=AD,
∴AB=BC=CD=AD,
∴四边形ABCD为菱形,故此选项正确;
故正确的有3个,
故选:C.
点评:此题主要考查了线段垂直平分线的性质以及菱形的判定和全等三角形的判定等知识,熟练应用菱形的判定方法是解决问题的关键.
分析:根据菱形的判定方法有三种:①定义:一组邻边相等的平行四边形是菱形;②四边相等的四边形是菱形;③对角线互相垂直平分的四边形是菱形分别判定即可,
解答:
 证明:①当AC⊥BD、OC=OA,不能确定BO是否等于DO,故不能判定四边形ABCD为菱形,故此选项错误;
证明:①当AC⊥BD、OC=OA,不能确定BO是否等于DO,故不能判定四边形ABCD为菱形,故此选项错误;②∵∠1=∠2=∠3=∠4
∴AB=AD,BC=CD,
在△ABD和△CBD中,
∵
 ,
,∴△ABD≌△CBD,
∴AB=BC,AD=CD,
∴AB=BC=AD=CD;
故四边形ABCD为菱形,故此选项正确;
③∵OA=OC、OB=OD,
∴四边形ABCD为平行四边形,
又∵AC⊥BD,
∴平行四边形ABCD为菱形,故此选项正确;
 ④∵AB=BC=CD,AC⊥BD,
④∵AB=BC=CD,AC⊥BD,∴在Rt△BOC和Rt△DOC中,
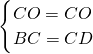
∴Rt△BOC≌Rt△DOC(HL),
∴BO=DO,
∴在Rt△ABO和Rt△ADO中,

∴△ABO≌△ADO(SAS),
∴AB=AD,
∴AB=BC=CD=AD,
∴四边形ABCD为菱形,故此选项正确;
故正确的有3个,
故选:C.
点评:此题主要考查了线段垂直平分线的性质以及菱形的判定和全等三角形的判定等知识,熟练应用菱形的判定方法是解决问题的关键.

练习册系列答案
 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案
相关题目
 (2013•来宾)如图,AB=AC,D,E分别是AB,AC上的点,下列条件中不能证明△ABE≌△ACD的是
(2013•来宾)如图,AB=AC,D,E分别是AB,AC上的点,下列条件中不能证明△ABE≌△ACD的是 如图下列条件
如图下列条件
