题目内容
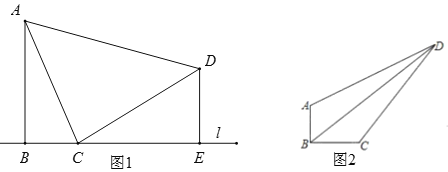
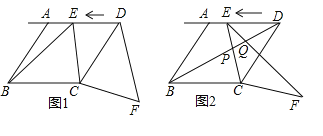
【题目】阅读下面材料:小昊遇到这样一个问题:如图1,在△ABC中,BE是AC边上的中线,点D在BC边上,![]() ,AD与BE相交于点P,求
,AD与BE相交于点P,求![]() 的值.
的值.
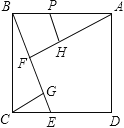
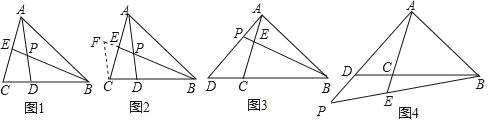
小昊发现,过点C作CF∥AD,交BE的延长线于点F,通过构造△CEF,经过推理和计算能够使问题得到解决(如图2).
请回答:写出![]() 的值.
的值.
参考小昊思考问题的方法,解决问题:
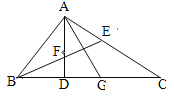
(1)如图3,在△ABC中,点D在BC的延长线上,![]() ,点E在AC上,且
,点E在AC上,且![]() .求
.求![]() 的值;
的值;
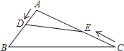
(2)如图4,在△ABC中,点D在BC的延长线上,![]() ,点E在AC上,且
,点E在AC上,且![]() ,直接写出
,直接写出![]() 的值.
的值.
【答案】![]() ;(1)
;(1)![]() ;(2)
;(2)![]()
【解析】
如图2,过点C作CF∥AD,交BE的延长线于点F,易证△AEP≌△CEF,根据全等三角形的性质可得AP=FC,又因PD∥FC,可得△BDP∽△BCF,由相似三角形的性质可得![]() ,由此即可求得
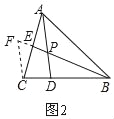
,由此即可求得![]() 的值.(1)如图3,过A作AF∥BC,交BP延长线于点F,可得△AFE∽△CBE,根据相似三角形的性质可得
的值.(1)如图3,过A作AF∥BC,交BP延长线于点F,可得△AFE∽△CBE,根据相似三角形的性质可得![]() ,设AF=3x,BC=2x,由
,设AF=3x,BC=2x,由![]() 可得BD=3x,所以AF=BD=3x,再证明△AFP∽△DBP,即可得
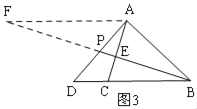
可得BD=3x,所以AF=BD=3x,再证明△AFP∽△DBP,即可得![]() ;(3)如图4,过C作CF∥AP交PB于F,可得△BCF∽△BDP,根据相似三角形的性质可得
;(3)如图4,过C作CF∥AP交PB于F,可得△BCF∽△BDP,根据相似三角形的性质可得![]() ,设CF=2x,PD=3x,再证明△ECF∽△EAP,可得
,设CF=2x,PD=3x,再证明△ECF∽△EAP,可得![]() ,所以AP=7x,AD=4x,即可求得
,所以AP=7x,AD=4x,即可求得![]() .
.
解:如图2,过点C作CF∥AD,交BE的延长线于点F,
∴∠F=∠APF,∠FCE=∠EAP,
∵BE为AC边的中线,
∴AE=CE,
∴△AEP≌△CEF,
∴AP=FC,
∵PD∥FC,
∴△BPD≌△BFC,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
(1)如图3,过A作AF∥BC,交BP延长线于点F,
∴△AFE∽△CBE,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
设AF=3x,BC=2x,
∵![]() ,
,
∴BD=3x,
∴AF=BD=3x,
∵AF∥BD,
∴△AFP∽△DBP,
∴![]() =
=![]() =1;
=1;
(2)如图4,过C作CF∥AP交PB于F,
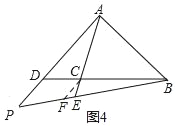
∴△BCF∽△BDP,
∴![]() ,
,
设CF=2x,PD=3x,
∵CF∥AP,
∴△ECF∽△EAP,
∴![]() ,
,
∴AP=7x,AD=4x,
∴![]() .
.

 阅读快车系列答案
阅读快车系列答案