题目内容
 已知,G是矩形ABCD的边AB上的一点,P是BC边上的一个动点,连接DG、GP,E、F分别是GD、GP的中点,当点P从B向C运动时,EF的长度
已知,G是矩形ABCD的边AB上的一点,P是BC边上的一个动点,连接DG、GP,E、F分别是GD、GP的中点,当点P从B向C运动时,EF的长度
- A.保持不变
- B.逐渐增大
- C.逐渐减少
- D.不能确定
C
分析:连接PD,根据E、F分别是GD、GP的中点,即EF是中位线,可得EF= DP,当点P从B向C运动时,DP长度逐渐减小,于是判断出EF长度的变化.
DP,当点P从B向C运动时,DP长度逐渐减小,于是判断出EF长度的变化.
解答: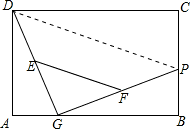 解:连接PD,
解:连接PD,
∵E、F分别是GD、GP的中点,
∴EF是中位线,
∴EF= DP,
DP,
当点P从B向C运动时,
DP长度逐渐减小,
故EF的长度也逐渐减小.
故选C.
点评:本题主要考查矩形的性质和三角形中位线定理的知识点,解答本题的关键是熟练运用三角形中位线定理,此题比较简单.
分析:连接PD,根据E、F分别是GD、GP的中点,即EF是中位线,可得EF=
 DP,当点P从B向C运动时,DP长度逐渐减小,于是判断出EF长度的变化.
DP,当点P从B向C运动时,DP长度逐渐减小,于是判断出EF长度的变化.解答:
 解:连接PD,
解:连接PD,∵E、F分别是GD、GP的中点,
∴EF是中位线,
∴EF=
 DP,
DP,当点P从B向C运动时,
DP长度逐渐减小,
故EF的长度也逐渐减小.
故选C.
点评:本题主要考查矩形的性质和三角形中位线定理的知识点,解答本题的关键是熟练运用三角形中位线定理,此题比较简单.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
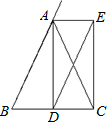 21、已知:如图,△ABC中,AB=AC,AD是BC边上的高,AE是△BAC的外角平分线,DE∥AB交AE于点E,求证:四边形ADCE是矩形.
21、已知:如图,△ABC中,AB=AC,AD是BC边上的高,AE是△BAC的外角平分线,DE∥AB交AE于点E,求证:四边形ADCE是矩形. 24、如图,已知:AD是△ABC中BC边的中线,则S△ABD=S△ACD,依据是
24、如图,已知:AD是△ABC中BC边的中线,则S△ABD=S△ACD,依据是
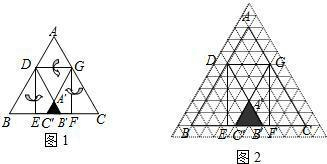 三角形A′B′C′的面积,并写出m的取值范围.(直接写出结果)
三角形A′B′C′的面积,并写出m的取值范围.(直接写出结果) 如图,已知四边形ABCD是平行四边形,下列结论中不正确的是( )
如图,已知四边形ABCD是平行四边形,下列结论中不正确的是( )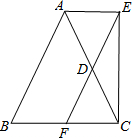 已知,如图在△ABC中,AB=AC,点D是AC的中点,直线AE∥BC,过D点作直线EF∥AB分别交AE、BC于点E、F,求证:四边形AECF是矩形.
已知,如图在△ABC中,AB=AC,点D是AC的中点,直线AE∥BC,过D点作直线EF∥AB分别交AE、BC于点E、F,求证:四边形AECF是矩形.