题目内容
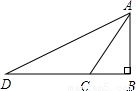
(2003•天津)在△ABC中,已知AB=2a,∠A=30°,CD是AB边的中线,若将△ABC沿CD对折起来,折叠后两个小△ACD与△BCD重叠部分的面积恰好等于折叠前△ABC的面积的 ,有如下结论:
,有如下结论:①AC边的长可以等于a;
②折叠前的△ABC的面积可以等于
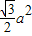 ;
;③折叠后,以A、B为端点的线段AB与中线CD平行且相等.
其中,正确结论的个数是( )
A.0个
B.1个
C.2个
D.3个
【答案】分析:①假设AC=a成立,根据等腰三角形的性质及图形折叠的性质可求出四边形AB1DC为平行四边形,再根据平行四边形的性质及三角形的面积公式求解;
②假设S△ABC=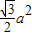 成立,再由△ABC的面积公式可求出AC=
成立,再由△ABC的面积公式可求出AC=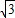 a,根据三角形的三边关系可求出∠B=60°,由平行四边形的判定定理可求出四边形AB2CD为平行四边形,再根据平行四边形的性质及三角形的面积公式求解;
a,根据三角形的三边关系可求出∠B=60°,由平行四边形的判定定理可求出四边形AB2CD为平行四边形,再根据平行四边形的性质及三角形的面积公式求解;
③综合①②可知,以A、B为端点的线段AB与中线CD平行且相等.
解答: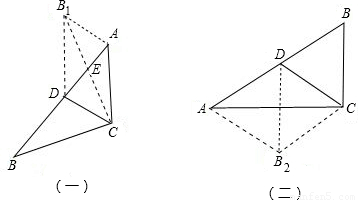 解:对于结论①,若AC=a成立,如图(一),在△ACD中,由∠CAD=30°,AD=a,
解:对于结论①,若AC=a成立,如图(一),在△ACD中,由∠CAD=30°,AD=a,
∴∠ADC= (180°-∠CAD)=75°,
(180°-∠CAD)=75°,
∠CDB=180°-∠ADC=105°,
而∠CDB1=∠CDB
∴∠B1DA=105°-75°=30°,
∴AC∥B1D,
∵B1D=BD=a=AC,
∴四边形AB1DC为平行四边形.
∴S△CED= S△ACD=
S△ACD= S△ABC,满足条件,即AC的长可以等于a,故①正确;
S△ABC,满足条件,即AC的长可以等于a,故①正确;
对于结论②,若S△ABC=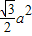 ,
,
∵S△ABC= AB•AC•sin∠CAB,
AB•AC•sin∠CAB,
∴AC=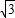 a,
a,
∵AC=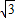 a,∠B=60°,如图(二),
a,∠B=60°,如图(二),
∴∠CDB=60°=∠DCB2,
∴AD∥B2C,
又∵B2C=BC=a=AD,
∴四边形AB2CD为平行四边形,
∴S△CFD= S△ACD=
S△ACD= S△ABC,满足条件,即S△ABC的值可以等于
S△ABC,满足条件,即S△ABC的值可以等于 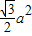 ,故②正确;
,故②正确;
对于结论③,由平行四边形AB1CD或平行四边形AB2CD,显然成立,故③正确.
故选D.
点评:本题考查的是翻折变换的性质及平行四边形的性质,熟知折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等的知识是解答此题的关键.
②假设S△ABC=
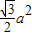 成立,再由△ABC的面积公式可求出AC=
成立,再由△ABC的面积公式可求出AC=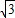 a,根据三角形的三边关系可求出∠B=60°,由平行四边形的判定定理可求出四边形AB2CD为平行四边形,再根据平行四边形的性质及三角形的面积公式求解;
a,根据三角形的三边关系可求出∠B=60°,由平行四边形的判定定理可求出四边形AB2CD为平行四边形,再根据平行四边形的性质及三角形的面积公式求解;③综合①②可知,以A、B为端点的线段AB与中线CD平行且相等.
解答:
 解:对于结论①,若AC=a成立,如图(一),在△ACD中,由∠CAD=30°,AD=a,
解:对于结论①,若AC=a成立,如图(一),在△ACD中,由∠CAD=30°,AD=a,∴∠ADC=
 (180°-∠CAD)=75°,
(180°-∠CAD)=75°,∠CDB=180°-∠ADC=105°,
而∠CDB1=∠CDB
∴∠B1DA=105°-75°=30°,
∴AC∥B1D,
∵B1D=BD=a=AC,
∴四边形AB1DC为平行四边形.
∴S△CED=
 S△ACD=
S△ACD= S△ABC,满足条件,即AC的长可以等于a,故①正确;
S△ABC,满足条件,即AC的长可以等于a,故①正确;对于结论②,若S△ABC=
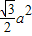 ,
,∵S△ABC=
 AB•AC•sin∠CAB,
AB•AC•sin∠CAB,∴AC=
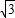 a,
a,∵AC=
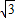 a,∠B=60°,如图(二),
a,∠B=60°,如图(二),∴∠CDB=60°=∠DCB2,
∴AD∥B2C,
又∵B2C=BC=a=AD,
∴四边形AB2CD为平行四边形,
∴S△CFD=
 S△ACD=
S△ACD= S△ABC,满足条件,即S△ABC的值可以等于
S△ABC,满足条件,即S△ABC的值可以等于 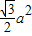 ,故②正确;
,故②正确;对于结论③,由平行四边形AB1CD或平行四边形AB2CD,显然成立,故③正确.
故选D.
点评:本题考查的是翻折变换的性质及平行四边形的性质,熟知折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等的知识是解答此题的关键.

练习册系列答案
相关题目
 ,有如下结论:
,有如下结论: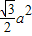 ;
;



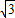 ≈1.732).
≈1.732).