题目内容
【题目】如图，在四边形ABCD中，已知AB=4cm，BC=3cm，AD=12cm，DC=13cm，∠B=90°，求四边形ABCD的面积。
【答案】解：连接AC，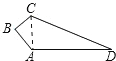
∵∠B=90°
∴AC2=AB2+BC2=16+9=25
∵AD2=144，DC2=169
∴AC2+AD2=DC2
∴CA⊥AD
∴S四ABCD=S△ABC+S△ACD=
×3×4+×12×5=36cm
【解析】连接AC，先根据直角三角形的性质得到AC边的长度，再根据三角形ACD中的三边关系可判定△ACD是Rt△，把四边形分成两个直角三角形即可求得面积．
【考点精析】本题主要考查了勾股定理的逆定理的相关知识点，需要掌握如果三角形的三边长a、b、c有下面关系：a2+b2=c2，那么这个三角形是直角三角形才能正确解答此题．
练习册系列答案
相关题目
