题目内容
两个相似三角形对应高的比为 2：3，且已知较小的三角形的面积为4，则较大的三角形的面积为________．
9
分析：先根据相似三角形对应高的比得出其相似比，再设较大的三角形的面积为S，根据相似三角形的性质即可得出结论．
解答：∵两个相似三角形对应高的比为 2：3，
∴相似三角形的相似比为2：3，
设较大的三角形的面积为S，则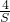
=（
）2，解得S=9．
故答案为：9．
点评：本题考查的是相似三角形的性质，即相似三角形面积的比等于相似比的平方．
分析：先根据相似三角形对应高的比得出其相似比，再设较大的三角形的面积为S，根据相似三角形的性质即可得出结论．
解答：∵两个相似三角形对应高的比为 2：3，
∴相似三角形的相似比为2：3，
设较大的三角形的面积为S，则
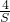=（）2，解得S=9．故答案为：9．
点评：本题考查的是相似三角形的性质，即相似三角形面积的比等于相似比的平方．
练习册系列答案
相关题目
两个相似三角形对应高之比为2：3，则它们的面积比为（ ）
A、
| ||||
| B、2：3 | ||||
| C、4：9 | ||||
| D、无法确定 |